こんにちは、今回も前回に引き続き、
- 大学以降の物理はどんな内容を勉強するのか。
- 現代物理学の分野ってどんなことがあるのか
について、紹介していきたいと思います。
量子力学、統計力学、特殊相対論について、紹介していきたいと思います。
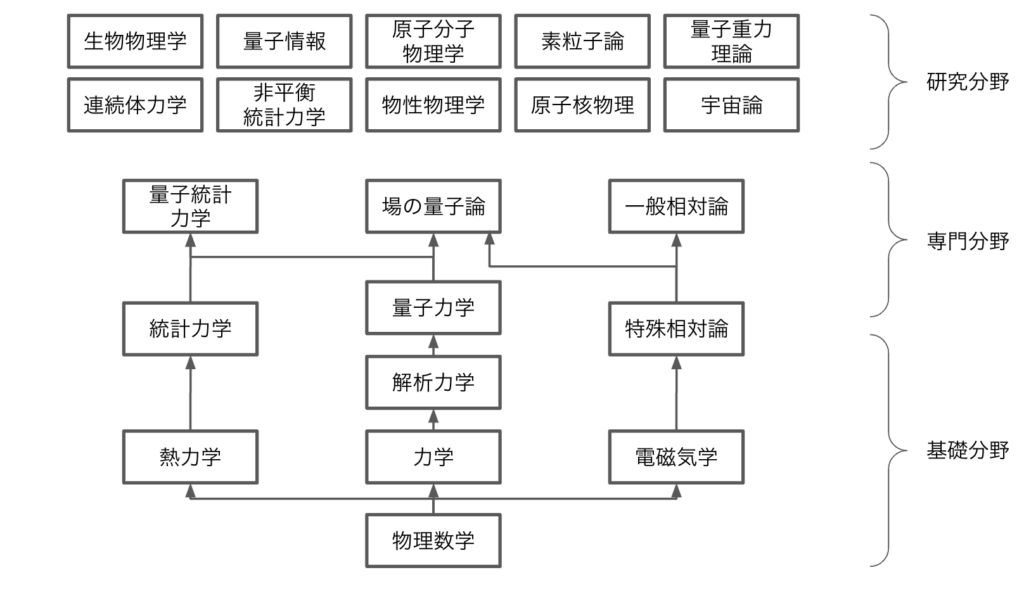
上図の注意点はこちらを参照してください。
- 量子力学
現代物理学の金字塔です。直観に反する理論なので、数式を駆使して論理を積み重ねていく分野です。20世紀初めには、物理学は(解析)力学、電磁気学、熱力学をもって完成した理論と認識されていました(これを古典力学と言います)。しかしどうしても上記の物理学では説明できない実験事実が出てきました。黒体輻射や光電効果がその例です。
これを解決するために提唱されたのがハイゼンベルクの行列力学やシュレーディンガーの波動力学です。
古典力学では、粒子は空っぽの空間の中を時々刻々飛び回り、その瞬間瞬間は確定した状態をもつイメージですが、量子力学では粒子的性質と波動的性質を持ち合わせていて、粒子の状態は無限次元ヒルベルト空間のベクトル(状態ベクトル)として記述されます。物理量は演算子(または作用素ともいう)に置き換わり、演算子の状態ベクトルに対する固有値が観測され、その固有値の選定は確率的になる、という古典物理での世界観をがらっと変えるものになってます。
このような世界観を記述するため、量子力学で使う数学も高度になります。線形代数や偏微分方程式を駆使します。数学的にさらに一歩踏み込むには関数解析という数学の分野の知識が必要になる場合もあります。
今や量子力学は物理学を超えて様々な分野に応用されています。化学の分野では化学結合や化学反応の原理的理解に応用され、レーザーの分野でも量子工学という名前で応用されています。コンピュータの基盤となる半導体の設計も量子力学が用いられています。さらに直接量子力学効果を情報分野に応用した、量子コンピュータも産学どちらもさかんに研究開発がすすんでおり、機械学習に続くブレイクスルーになるかと思われます。
直観に反する分野であることから、トンデモ理論に結びつけられやすいですが、神秘的な学問ではなく現代社会を支える科学技術の基盤となっている学問です。 - 統計力学
ミクロスケールとマクロスケールをつなぐ学問です。すでに整備されていた熱力学から得られるマクロな結果を、力学法則に従う多数の粒子系に統計処理を施して導出しようとする理論です。ボルツマンはミクロな系の状態数\(W\)とマクロな状態量であるエントロピー\(S\)をつなぐ式\(S = k_B\log W\)を見つけたことから始まります。
また当時(解析)力学と熱力学に深い溝があり、熱力学第二法則(孤立系のエントロピーは増大する)とポアンカレの再帰定理(孤立系では任意の精度で初期状態の近傍に戻る)との一見矛盾する点を数学者から指摘されていましたが、これもボルツマンにより分子混沌仮説の元、どちらも相容れないものでないことを証明しています。(H定理)
ミクロな性質からマクロな性質を導くには、原理的には\(10^{23}\)個の連立した運動方程式を解けばよいのですが、力学では三体の相互作用した問題ですら、解析的に解くことは不可であることが証明されているため、困難です。かたや数値計算するにも現代のスパコンを使っても宇宙の年齢をはるかに超える時間がかかるので、実質不可です。このため統計力学が必要となるのです。
ミクロ系に統計処理をすればなんとかマクロの性質を導き出せるのですが、これは簡単ではなく、平衡状態にない現象に関してはほとんど理解できてないのが現状です。この世界の現象は非平衡状態の変化によるものばかりなので、統計力学は完成された学問ではなく、まだまだ発展する分野とも言えます。
現代では機械学習でのボルツマンマシンの元ネタとして使われていたり、情報統計力学という情報理論や統計学との学際領域などもあります。 - 特殊相対論
有名なアインシュタインが1905年に発表した理論で、量子力学に並ぶ現代物理学の金字塔のひとつです。電磁気学によると光は電磁波であることが示されていますが、光と同じ速さの乗り物で乗っていて、そこから光を見るとどう見えるか、という思考実験から、光速はいかなる速さの乗り物から見ても同じ速度になること、それぞれの速さで動く系の物理法則は等価であることを基本原理として特殊相対性理論が作られました。
特殊相対論の登場により力学は変更を受けることになります。それまでの世界観は時間と空間は別々の存在で、粒子は空っぽの空間の中を飛び回る、つまり位置\(x\)は時間\(t\)の関数で\(x(t)\)と記述できる描像でした。しかし相対論では時間と空間は等価であるとし、空間に時間を加えた4次元ベクトルで記述するようになり、運動量も4次元で記述されます。有名な式\(E=mc^2\)が得られるようになります。
上記の4次元で記述することで、光速に近づくにつれ、時間の流れが遅れるように見えたり、物体の大きさが縮んで見えたりするという、直観に反した結果が得られます。これも数式を使って論理を積み重ねることによって理解されます。
上記を数学的に記述するためテンソルという概念が使われます。これはベクトルの拡張した概念で、初見ではなかなか難しいです。
今回は以上になります。もしよろしければ以下の記事もご覧ください。
- 現代物理学への招待1 ー物理数学、力学、熱力学、電磁気学ー
- 現代物理学への招待2 ー量子力学、統計力学、特殊相対論ー ※本稿
- 現代物理学への招待3 ー場の量子論、量子統計力学、一般相対論ー
- 現代物理学への招待4 ー素粒子論、量子重力理論、宇宙論ー
- 現代物理学への招待5 ー原子核物理、原子分子物理、物性物理ー
- 現代物理学への招待6 ー量子情報、非平衡統計力学、生物物理、連続体力学ー
最後まで読んでくださりありがとうございます。
質問等はコメント欄かお問い合わせにてよろしくおねがいいたします。
「現代物理学への招待2」への2件のフィードバック
コメントは受け付けていません。