こんにちは、今回も前回に引き続き、
- 大学以降の物理はどんな内容を勉強するのか。
- 現代物理学の分野ってどんなことがあるのか
について、紹介していきたいと思います。
今回は場の量子論からです。
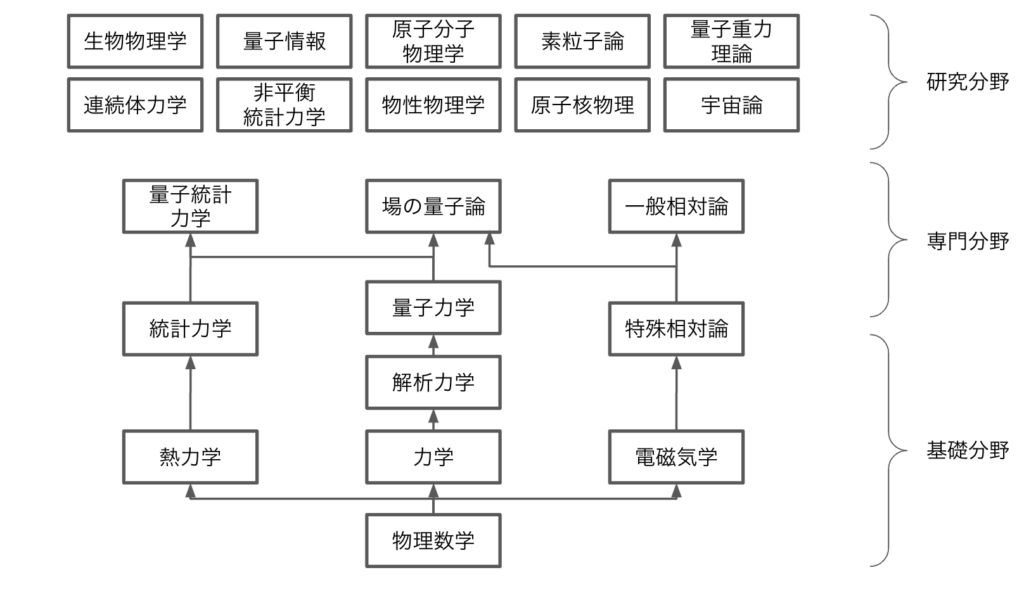
- 場の量子論
量子力学はミクロな粒子を記述する理論ですが、粒子が光速になるケースは記述できません。相対論的効果を考慮する必要となります。Diracは特殊相対論と量子力学と合わせた相対論的量子力学を構築しましたが、粒子のエネルギーを計算すると、負のエネルギーが出てきてしまい解釈に困るものでした。その後多数の物理学者により、物理的実体に「場」という概念を使い、場が高いエネルギーへ励起することで粒子は生成し、場が低いエネルギーへ遷移することで粒子は消滅をするような描像に至りました。
そのように発展した場の量子論は、現代物理学で最も精度の高い理論です。電子の異常磁気モーメントという物理量があるのですが、この実験値と理論値が有効数字10桁以上一致するという驚異的な精度を誇ります。物理学を超えて他の分野をみても、これを超える精度の理論はないかと思われます。
今や素粒子を記述するために発達した場の量子論は、原子核物理や物性物理、量子統計力学etc.にも応用され、最先端分野の基盤となる理論になってます。
場の量子論で使われる数学も多岐に渡ります。スピノル代数、グラスマン代数、群論、経路積分etc.とかなり広範囲です。(経路積分の数学的基礎は現在も整備中です。)
量子力学はノイマンにより数学的に疑義のない厳密な理論として整備されていますが、場の量子論は数学的(数理物理学的)にはまだまだ不完全です。「場」の自由度は無限大となります。この無限大の扱いが数学者から見るとまだまだのようで、数理物理学では場の量子論を数学的に厳密に定義するのが、主要テーマの一つになってます。Wightmanの公理系から得られる「CPT定理」や「スピンと統計性の関係」など、一定の結果を得られてはますが、現在も完成してはいません。
ちなみに原子核を記述する場の量子論の方程式にヤン・ミルズ方程式というものがありますが、この一般解の存在の証明に100万ドルの懸賞金がかけられてます。 - 量子統計力学
その名の通り、量子力学に従う粒子を量子といいますが、それらがたくさん集まった系(量子多体系といいます)を記述する分野です。量子の種類として、フェルミ粒子とボーズ粒子の2つがあるのですが、フェルミ粒子は1つの状態に1粒子しか存在できず、一方ボーズ粒子は同一の状態にいくらでも存在することができます。
化学の分野で1つの軌道には2つの電子しか入らない、という性質がありましたが、これはフェルミ粒子の性質によるものです。
※電子にはスピンという自由度があり、「↑」と「↓」という状態を取れ、「↑」の電子と「↓」の電子は別の状態となるため、1つの軌道に2つ入れます。
これらの粒子が集まった系を超低温or超高圧にすると、非常に特異な現象が発生します。超伝導や超流動がそれです。それらを理論的に説明するのが量子統計力学という分野になります。
超伝導の微視的理論はBCS理論と言われているのですが、これを素粒子の分野に応用したのが、南部陽一郎で、BCS理論をヒントに自発的対称性の破れの概念に到達し、2008年にノーベル賞を受賞してます。
場の量子論で得られた描像は量子統計力学でも都合がよく、さらに数学的にも時間座標に対してある線型変換をするだけで、そのまま量子統計力学に適用できます。量子統計力学と場の量子論は非常に相性がよいです。 - 一般相対性理論
特殊相対性理論では、平坦な時空間しか扱えなかったのですが、それを改善した理論になります。一般相対論では、ある質量を物体があると、その周りの時空が歪み、その歪みが重力である、という描像です。
太陽はめちゃくちゃ質量があるので、その周りの時空が歪み、重力が発生します。この重力によって地球は公転している、という感じです。地球の周りも時空が歪んではいますが、太陽の存在による歪みからすると小さすぎるので、無視できる、といった感じです。
時空の歪みを記述するために、数学的には4次元のリーマン幾何学を用います。これがテンソルまみれで計算がなかなかえぐいです。アインシュタイン方程式とよばれているのですが、これは2階のテンソル方程式で、バラせば10個の偏微分連立方程式となるシロモノで、一般の場合解析的に解くことは困難です。特別な条件を課すことで、いくつかの場合のみ解かれています。
そのひとつがシュワルツシルト解でブラックホールを記述するのに用いられています。
一般相対性理論はかなりスケールの大きな話に聞こえますが、実は現代社会でも活躍してます。携帯電話にGPSという機能がありますが、人工衛星での重力と地球上の重力に差があるため、そのままではGPSは使い物になりません。重力の差によって数十キロ程度の誤差が生じてしまうようで、これを補正するために、一般相対性理論を使っています。
2016年に重力波が実験で検出されましたが、これも一般相対性理論による結果です。
非常に重い星2つがくるくる回っていると、その周りの時空の歪みも周期的に振動するようになります。これが重力波です。アインシュタインが一般相対性理論を発表して100年後に示されるとは因果なものですね。
今回はこれぐらいにしておきます。なるべく深くは触れないようにしましたが、少し難しい部分もあるかもしれません。
もしよろしければ以下の記事もご覧ください。
- 現代物理学への招待1 ー物理数学、力学、熱力学、電磁気学ー
- 現代物理学への招待2 ー量子力学、統計力学、特殊相対論ー
- 現代物理学への招待3 ー場の量子論、量子統計力学、一般相対論ー ※本稿
- 現代物理学への招待4 ー素粒子論、量子重力理論、宇宙論ー
- 現代物理学への招待5 ー原子核物理、原子分子物理、物性物理ー
- 現代物理学への招待6 ー量子情報、非平衡統計力学、生物物理、連続体力学ー
最後まで読んでくださりありがとうございます。
質問などはコメント欄かお問い合わせにてよろしくおねがいいたします。
「現代物理学への招待3」への6件のフィードバック
コメントは受け付けていません。