サラリーマンが場の量子論を勝手に解説する無謀な記事３

今回量子化について、見ていきます。

3)場の量子化

前回の投稿で場$\psi$とその共役運動量$\pi$のポアソン括弧

$$\{\psi(t,x),\pi(t,y)\}=\delta(x-y)$$

になることを示しました。これを量子化するには

• $\psi,\pi$を演算子(作用素)に変更する
• ポアソン括弧を交換関係にする。

という手続きで実施できます。これを正準量子化といいます。

つまり

$$[ \hat{\psi},\hat{\pi}]=i\hbar\delta(x-y)$$

とするかたちとなります。ここで$\hbar$はディラック定数で$1.05457\dots \times 10^{-34}$J・sという小さな値です。
実は物理的には手続きはこれだけなんですが、数学的に深入りすると大変になります。まず場とその運動量を演算子or作用素にするとなると、その定義域を定義する必要があります。これはヒルベルト空間の無限直和からなるフォック空間なるものを導入することになり、なかなかエグめになります。詳細は新井朝雄さんの「フォック空間と量子場」を参照してみてください。

実は上記のやり方は場の量子化ではあまり使われません。というのも場の共役運動量$\pi$はラグランジアン密度$\mathscr{L}$を$\partial_t\psi$で変分したものですが、$\partial_t\psi$という時間微分した場だけが出てきて、これだけ特別視してる感があります。ラグランジアン密度は$\mathscr{L}(\psi,\partial_\mu \psi)$で場$\psi$と時間微分/空間微分$\partial_\mu\psi$の関数でしたから、時間微分$\partial_t\psi$で変分した量だけを取りあげるのは、ちぐはぐ感があるのです。
※物理学的にいうとラグランジアンは相対論的共変性が見えやすいが、ハミルトニアンはそれが見えにくい、と表現します。

そこで使われるのが経路積分(or汎関数積分)という手法です。これは連続無限個の積分変数ですべて積分を実行するという荒技です。一般の場合、このような連続濃度の積分測度は存在しないことが数学的に証明されてしまっているのですが、ある条件下ではその存在を証明できるようです。

この経路積分について見ていきます。
場「$\psi$」がある状態「$\psi_1$」から別の状態「$\psi_2$」に遷移するときの遷移確率を考えます。
このとき$\psi_1\rightarrow \psi_2$の遷移の仕方は、直線的に遷移するものもあれば、遠回りして遷移するケースもあり、無限に存在します。経路積分はそれらを「経路」を全部足し合わせる、つまり「積分」する、というものです。

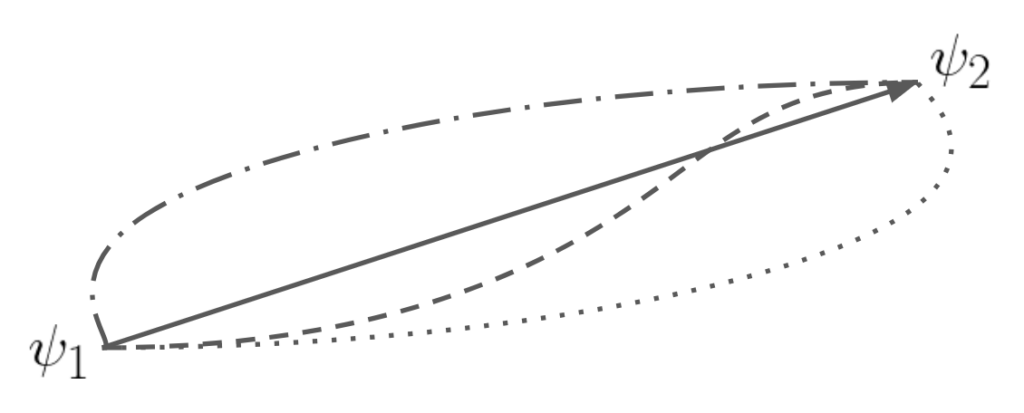
とはいえ、すべての経路が同確率で発生するとは考えづらいので、何かしらの加重平均をとる必要があります。
この加重平均の係数は$S$を作用として、$\exp\left\{ iS/\hbar \right\}$として与えられます(なぜそうなるかは別の記事に書きます)。作用$S$は
$$S=\int d^4x \mathscr{L} ( \psi,\partial_{\mu}\psi )$$
でしたので、$\psi_1$から$\psi_2$への遷移確率を$\left \langle \psi_2 | \psi_1 \right \rangle$で表すと、

$$\left \langle \psi_2 | \psi_1 \right \rangle = \prod_{\psi\in\Psi}\int d\psi \exp\left( \frac{i}{\hbar} \int d^4 x \mathscr{L}(\psi,\partial_\mu \psi)\right) \tag{1}$$

とかけます。ここで、$\Psi$は$\psi_1$から$\psi_2$へ遷移する際にとりうる場全体の集合で、関数空間を表します。つまり(1)式の意味は「加重平均を$\exp \{iS/\hbar\}$として、とりうる場$\psi$をすべて足し合わせた量が、$\psi_1$から$\psi_2$への遷移確率になる」となります。
ここで$\prod_{\psi\in\Psi}\int d\psi$を$\int D\psi$と略記して

$$\left \langle \psi_2 | \psi_1 \right \rangle = \int D\psi \exp\left( \frac{i}{\hbar} \int d^4 x \mathscr{L}(\psi,\partial_\mu \psi)\right) \tag{2}$$

と書きます。これを(ファインマンの)経路積分と呼びます。

この式を物理学的に吟味してみます。加重平均の係数$\exp(iS/\hbar)$は振動関数の形をしています。変分原理の説明でも少ししましたが、物理的に実現するものは作用が最小になる場合なので、$S=\int d^4x \mathscr{L}(\psi,\partial_\mu\psi)$が最小値をとる付近では加重平均の係数$\exp(iS/\hbar)$はゆったりした変化で、その時の$\psi$は積分に大きく寄与します。
一方物理的に実現しない作用は大きくなるので、$\exp(iS/\hbar)$は激しく振動するので、その時の$\psi$は打ち消しあい、積分にほとんど寄与しなくなります。
つまり物理的に実現する$\psi$が大きく積分に寄与し、逆に物理的に実現しにくい$\psi$はほとんど積分に寄与しない、といういい感じの式になってます。

かなり直感的な説明ですが、以上です。この積分測度$D\psi$は連続濃度の関数空間$\Psi$の全ての元に対して積分を実行するので、一般にこの極限が存在するかは吟味する必要があります。数学的に厳密に議論しようとすると関数解析学や測度論的確率論の知識が必要になってきて、げふぁ、な状況になります。このあたりの詳細を知りたい場合は、新井さんの「量子数理物理学における汎関数積分法」を参照ください。

最後まで読んでくださりありがとうございます。
質問等はコメント欄かお問い合わせにてよろしくおねがいいたします。