現代物理学への招待６

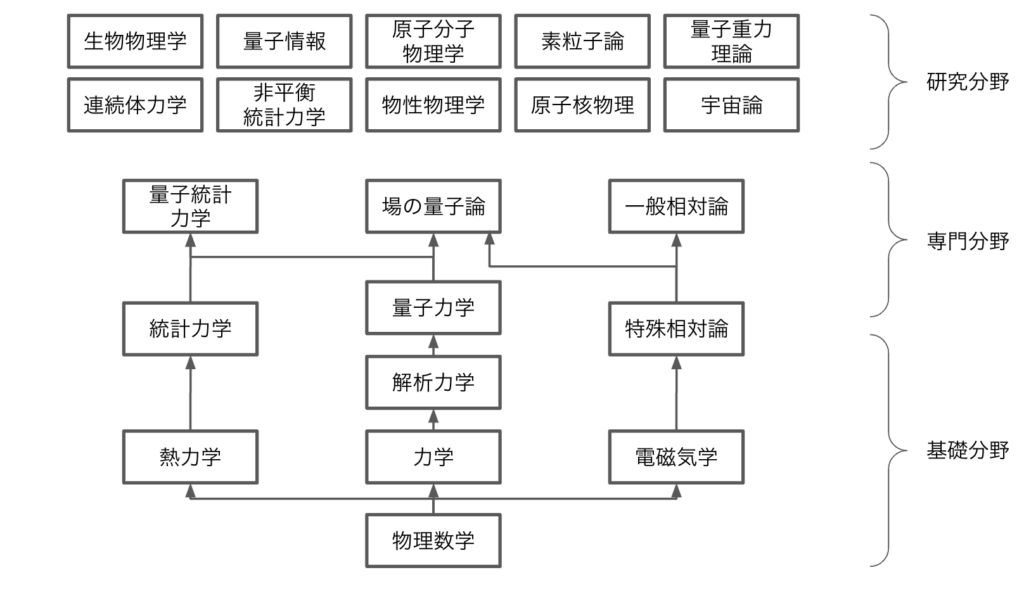
今回は量子情報から記載していきます

• 量子情報
  機械学習の次のブレイクスルーになると思われる、量子コンピュータの理論です。現在の計算機も半導体の性質を評価する中で量子論が使われていますが、通常計算機の動作を設計する上ではブール代数で理想化され、量子論が顔を出すことはまずないです。
  量子コンピュータは計算機の動作自体に量子論を効果を取り込ませるものです。
  量子論は解の線型性を、「重ね合わせの原理」と言ってますが、これによりビット単位で並列計算ができるようになります。
  
  近年D-Wave社が量子コンピュータを納品したニュースが出てますが、これは従来から研究されてきた量子ゲートを用いた汎用機ではなく、量子アニーリングと呼ばれるもので、特定の問題に特化した専用機的扱いになります。とはいえ、計算原理に量子論が使われ、量子超越性がgoogleにより示されており、量子コンピュータであることに違いないです。なお量子超越性とは現在のコンピュータでは解くのに膨大な時間がかかる問題を量子コンピュータでは圧倒的に短時間で解けることを言います。
  
  量子コンピュータの出現は現代の生活においても、重大な影響を与えます。
  ネットショッピングなどで使われている暗号は公開鍵暗号などが使われていますが、これは大きい数の素因数分解に解くのに膨大な時間がかかることを利用したものですが、量子コンピュータでは素因数分解を比較的短時間で解くアルゴリズム(ショアのアルゴリズム)が知られています。つまり量子コンピュータが日常で使われはじめると、公開鍵暗号は使い物にならなくなります。
  
  そこで量子情報理論は新たな暗号理論も検討されています。量子暗号と呼ばれるもので、これは盗聴をほとんど確実に検出できるものです。最初はBB84というプロトコルが提案され現在までに様々な暗号方式が提唱されています。
  
  個人的に気になっているのはトポロジカル量子計算と呼ばれるものです。これはトポロジカル絶縁体の表面上でマヨラナフェルミオンが存在することが最近発見され、マヨラナフェルミオンを使って量子計算させるのがトポロジカル量子計算です。元々非可換エニオンとよばれる仮想的な粒子を用いて結び目理論の手法を使って量子計算させることが以前から研究されてきましたが、マヨラナフェルミオンが発見されたことにより、一気に実用化が期待できるようになってきてるようです。従来の量子コンピュータにおける量子状態は外部の摂動に敏感ですぐに壊れてしまいますが、トポロジカル量子計算は粒子の状態が位相幾何学的な性質によって、外部の摂動に強い堅牢性をもつため、実用性が高い（と勝手に思ってます。）Microsoft社がStationQという組織を立ち上げて、トポロジカル量子計算の実用に向けて研究を進めてるようで、その期待値が高いことが伺えます。
  
  いろいろ記載していくと量子情報だけで本一冊かける分量になるので、ここまでにします。
  
  
• 非平衡統計力学
  話変わって非平衡統計力学について、紹介していきます。
  現在、熱力学や統計力学が完全に記述できるのは、平衡系な系に対してのみであり、非平衡な系は未完成な状態となってます。
  非平衡な系を扱う際、まずは系全体は非平衡であるものの、局所的には平衡状態であることを仮定するものです。この手法は他の分野でもよく使われていて、例えば一般相対論は局所的には特殊相対論が成り立っているという要請から構築されてたりして、まずは局所的には既存が成り立つ的な仮定をおくのは常套手段です。
  局所的に平衡であることから出発して、非平衡な現象を扱う理論は線型応答理論と呼ばれ、日本の物理学者久保亮五によって整備されてます。ざっくりいえば、平衡状態のハミルトニアンに摂動項を加え、この摂動項が非平衡状態へ駆動させると考える理論です。場の量子論を線型変換(Wick回転)することで統計力学と結びつくことから、素粒子分野で実績のある場の量子論の摂動計算手法がそのまま使える点が大きな利点となってます。
  揺動散逸定理を通じて生体構造の解明を目指す生物物理学とも深い関係があります。
  
  非線型の平衡状態を扱う分野は、線型応答理論のような整備された理論を絶賛構築中となっているようです。
  
  
• 生物物理学
  生命の現象を物理学的手法を用いて解明する分野です。生命現象は非平衡系の最たる例なので、様々な手法を用いて、研究を進めている分野となります。この分野でも非平衡統計力学を通じて場の量子論的な手法も使われています。
  
  
• 連続体力学
  連続体とは原子や分子というミクロな状態を無視して、空間に連続的に存在する物体を扱う分野です。連続体は主に流体と剛体に分かれ、ざっくりいえば流体は力に対して変形し、剛体は変形しない理想化された概念となります。現実の物質を解析する際は状況に合わせて、どちらにみなして計算することになります。
  この分野の代表例のひとつが流体力学です。ナビエ・ストークスの式という有名な式がありますが、非線形微分方程式で相当複雑です。この解は一般解の証明できれば1億円もらえます。
  もうひとつの例が材料力学で、物体に力が加わった時、どの部分にどれだけの変形や破壊が生じるかを調べる分野です。土木工学や建築系の分野の基礎になってる分野となります。

生物物理学や連続体力学は非常に魅力的な分野ですが、私の専門からかなり離れている関係上、詳しい話はほとんどできてません。。ご容赦いただければと思います。

今回はここまでにします。もしよろしければ以下の記事もご覧ください。

• 現代物理学への招待１　ー物理数学、力学、熱力学、電磁気学ー　
• 現代物理学への招待２　ー量子力学、統計力学、特殊相対論ー　
• 現代物理学への招待３　ー場の量子論、量子統計力学、一般相対論ー
• 現代物理学への招待４　ー素粒子論、量子重力理論、宇宙論ー
• 現代物理学への招待５　ー原子核物理、原子分子物理、物性物理ー
• 現代物理学への招待６　ー量子情報、非平衡統計力学、生物物理、連続体力学ー　※本稿

最後まで読んでくださりありがとうございます。
質問等はコメント欄かお問い合わせにてよろしくおねがいいたします。