サラリーマンが測度論を勝手に解説する無謀な記事１

いきなりですが、測度論/ルベーグ積分のこころを解説していきたいと思います。
ルベーグ積分は解析学で最初の難関分野でして、専門外の私はかなり苦労しました。
　(今も完全に理解しているのか、と言われると疑問ですが、、汗)
この記事が同じように苦労している人の突破口になれば幸いでございます。

1. 無限集合の扱い

といいつつ、最初は集合、とくに無限集合についてです。もはや積分と全然関係ない感がありますが、実は測度論は集合論と深い関係があり、カントールの測度の深い考察から現代集合論のたたきができました。そのため集合論なしに測度論は語れないのです。

結論から言うと、無限集合には2種類存在します。それは
・可算集合
・非可算集合
です。例としては、
・可算集合：自然数全体の集合や、整数全体、有理数全体
・非可算集合：無理数全体や実数全体、複素数全体
となります。

この分類は感覚的に言うと、無限集合の元の数が、数えられるか否かなのかで分類したもので、イメージ的には可算集合は数えられるくらいの無限、非可算集合は数えられないくらいの無限といった感じです。毎度拙い図ですんませんが、以下がイメージ図です。

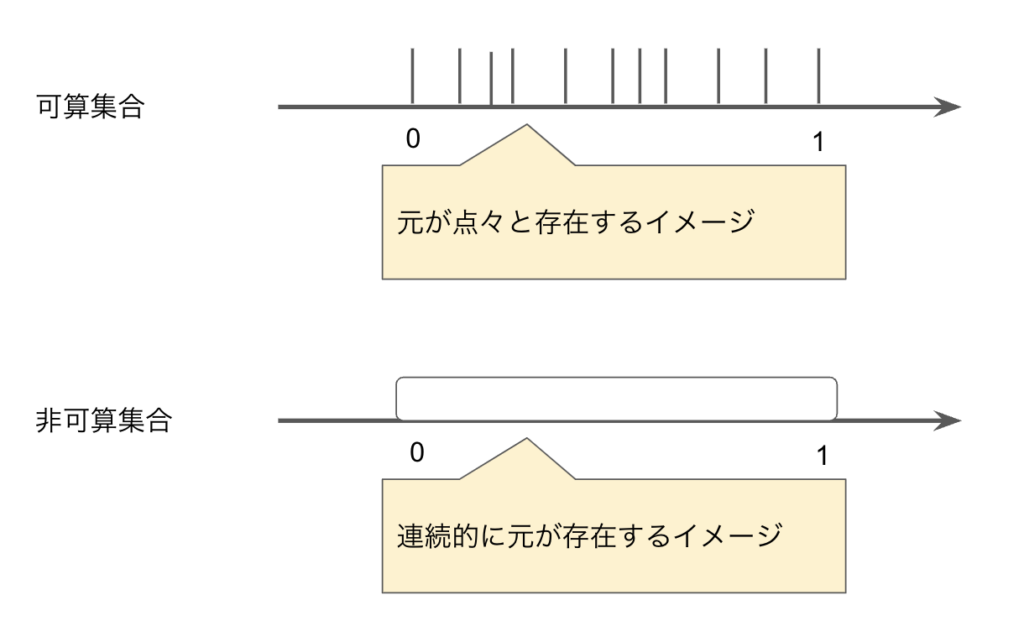
連続的に存在するというのは、開区間\((0,1)\)からテキトーに元\(x\)を選ぶと、区間\( (0,1)\)の分割方法は、
1)\((0,x)\cup [x,1)\)
2)\((0,x]\cup (x,1)\)
のいずれかになるよ、という意味合いです。
この分割の話は「デデキント切断」といい、数学的には分割1)or2)を満たすような集合を実数と定義します。

無限集合の元の「数」は数え切れないので、別の概念が必要で、「濃度」というもので表します。
無限集合\(A,B\)があったとき、同じ濃度であることは\(A,B\)の間に全単射(1対1の写像)が存在するとし、\(B\)の濃度が\(A\)の濃度以上であることは、単射\(f:A\rightarrow B\)が存在することと定義します。つまり自然数全体と整数全体の間には全単射が存在し、自然数全体から実数については全単射は存在せず、単射のみ存在することになります。
可算集合の無限と非可算集合の無限は、同じ「無限」であってもランクが全然違うことがわかります。

実数論について、これ以上は深入りしませんが、実数論は現代数学の基盤となるので、数学のガチ勢を目指すのであれば、一度はしっかり勉強することをお勧めします。数学は積み上げの分野なので、わからなくなったら前提となる分野に戻るのが一番の近道だったりします。
(と言ってる私は専門外のただの趣味勢ですがw)

2.測度

さて、集合の大きさを定義するのに、単純に元の数をとると無限集合の場合数え切れない、という問題がありました。特に非可算集合なんかはもはや数えることすらできない集合でした。そこでもう少しいい感じに集合の大きさを決める指標がないか、ということで考案されたのが「測度」になります。ここではルベーグ測度を例に話していきたいと思います。

区間\(\Omega=[0,1]\)を考えます。\(\Omega\)の集合の大きさを決めたいのですが、\(\Omega\)は非可算集合なので、元の数を数えることすらできません。
そこで、素朴に考えて「幅」を非可算集合の大きさにするのはどうか、というアイディアが出るかと思います。つまり\(\Omega=[0,1]\)の幅を\(1-0=1\)とする感じです。
「幅」を表す写像をKKDで\(\mu\)とおき、区間\([a,b]\)の幅を\(\mu([a,b])=b-a\)と表すことにします。
※KKD:カンと経験と度胸

幅を表す写像\(\mu\)の性質というか前提というかを考えてみます。

・区間\(\Omega\)の内部には例えば\([1/3,1/2]\)や\([0.3,0.5]\)、\([1/\sqrt{3},1/\sqrt{2}]\)など非常にたくさんの区間が存在しますが、\(\mu\)は、これらに対しても適用できると考えるのが普通です。\(\mu((1/3,1/2)) = 1/6\)、\(\mu((0.3,0.5))=0.2\)、\(\mu((1/\sqrt{3},1/\sqrt{2}))=1/\sqrt{2}-1/\sqrt{3}\)といった具合ですね。

・\(\mu\)の性質として、区間\([0.3,0.5]\)と区間\([0.7,0.8]\)をあわせた幅は、区間\([0.3,0.5]\)の幅と区間\([0.7,0.8]\)の幅の和になってほしいところです。式で書くと\(\mu([0.3,0.5]\cup [0.7,0.8])=\mu([0.3,0.5]) + \mu([0.7,0.8])\)となります。

・また区間\(\Omega\)の任意の区間\(A\)の補集合\(A^c\)もまた区間になってほしいです。例えば、\([0.2,0.3]\)の補集合は\([0,0.2) \cup (0.3,1]\)となり、区間になります。

・一点の幅は0です。\(\mu([a,a])=a-a=0\)といった感じです。

以上のことから、
・幅を定義できる区間は、区間\(\Omega\)自身とその内部に存在する区間を全て集めてきた集合。
・区間の補集合もまた区間
・区間と区間の和集合はまた区間
といった感じにまとめられ、幅は
・点のような区間でない幅は0
・重なってない区間の和集合の幅は、各区間の幅の和に等しい。
となります。これがσ加法族や測度の考え方に繋がっていきます。もう一段階推し進め上記の性質をもう少し数学的に書き直したのが以下です。

DEF.1 \(\sigma\)加法族
\(\Omega\)を空でない集合とする。\(\Omega\)の部分集合族\(\mathcal{F}\)が以下の性質を満たす時、\(\sigma\)加法族という：
・\(\phi \in \mathcal{F},\Omega \in \mathcal{F}\)
・\(A\in\mathcal{F}\)ならば、\(A^c\in \mathcal{F}\)
・\(\mathcal{F}\)の可算個の集合列\(\{A_j\}_{j=1}^{\infty}\)に対して、\(\bigcup_{j=1}^{\infty}A_j \in \mathcal{F}\)。
また集合の組\((\Omega,\mathcal{F})\)を可測空間という。

DEF.2 測度
\((\Omega,\mathcal{F})\)を可測空間とする。以下の性質をみたす写像\(\ \mu:\mathcal{F}\ni A\rightarrow \mu(A) \in[0,\infty)\)を測度という。：
・\(\mu(\phi)=0\)
・\(\mathcal{F}\)の互いに交わらない可算個の集合列\(\{A_j\}_{j=1}^{\infty}\)に対して、 \(\mu\left(\bigcup_{j=1}^{\infty}A_j\right)=\sum_{j=1}^{\infty}\mu(A_j)\)
可測空間\((\Omega,\mathcal{F})\)に測度\(\mu\)を加えた、\((\Omega,\mathcal{F},\mu)\)を測度空間という。

少しくどいかもですが、対応関係を少しかいておくと
区間：\(\Omega\)、\(\Omega\)に存在する区間：\(A_j\)、\(A_j\)全体の集合：\(\mathcal{F}\)、\(A_j\)の幅：\(\mu(A_j)\)といった感じになります。

数学的な定義に書き直す上で考え方が変わってます。それまでは区間や幅をざっと決めてこうであってほしい性質を上げていきましたが、逆に数学的な定義ではこうあってほしい性質をみたす対象であれば、区間や幅に限らずすべてσ加法族や測度とする、というものですね。こうすることで、区間や幅以外でもこうあってほしい性質を満たせば、すべて区間や幅と同じノリで扱えることになります。

気づいたら結構長くなってしまったので、本日はここまでにします。

最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問い合わせにてよろしくおねがいいたします。