集合論的にオブジェクト指向を考える

こんにちは、本日はオブジェクト指向を集合論の概念を用いて、独断と偏見で記述していきたいと思います。
本稿はこちらで紹介した児玉さんの「UMLモデリングの本質」を参考しています。

1)集合論における「関係」

まず集合論上の「関係」について。\(A,B\)を空でない集合とします。このとき二項関係\(R\)とは、
\[
R\subset A\times B
\]
なる直積\(A\times B\)の部分集合\(R\)が存在するときをいい、\(a\in A,b\in B\)に対して、\[
aRb
\]や\[
R(a,b)
\]等で表記します。二項関係のよく知られている例は、不等号「\(<\)」で、\(a< b\)と表記します。
(不等号は小学生のときから使っている記号でかなり見慣れているもので今更感満載ですが、典型的な二項関係の１種になります。)

さて、関係のうち特別な関係である「同値関係」について定義します。一言で言えば、反射的かつ対称的かつ推移的な二項関係は同値関係と呼ばれます。
集合\(M\)上の二項関係\(R\)について考えます。\(a,b,c\in M\)とすると
・反射律：\(aRa\)
・対称律：\(aRb\)ならば\(bRa\)
・推移律：\(aRb \ \& \ bRc\)ならば\(aRc\)
を満たす時、\(R\)は同値関係と呼び、\(\sim\)で表すことが多いです。

同値関係の例は、三角形の合同「\(\equiv\)」や等号「\(=\)」があります。

集合\(M\)に何かしらの同値関係「\(\sim\)」与えられると、「\(\sim\)」で\(M\)を分類することができます。これを\(\sim\)における商集合といい、\(M/\sim\)で表します。

\(M/\sim\)の元は「同値類」とよばれ、
\[
[a]\equiv \left\{m \in M \mid m \sim a \right\}\in M/\sim
\]
で定義します。このとき\(a\)を代表元といい、\([a]\)を同値類もしくはクラスと呼びます。

簡単な図でいうと以下のようなイメージです。

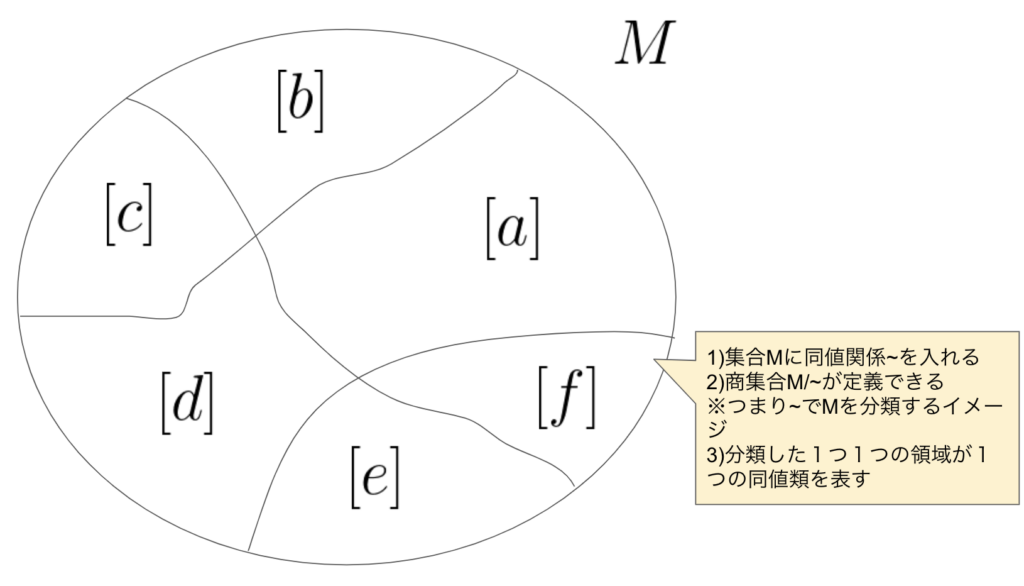
ちなみに同値類は\(M\)を直和分解するとも見ることができます。同値類の集合を
\[
\left\{[a] \in M/\sim \mid a=\{a_1,a_2,..,a_n\} \right\}
\]
とすれば、
\[
M= \bigcup_{i=1}^{n}[a_i]
\]
が成立することになります。これは同値類が\(M\)の元を追加したり、消したりせず、ただ分類のみ行うイメージでしたから、分類したものを全て合わせればまた\(M\)になる、という意味合いです。

同値類というとなにやら難しい感がありますが、例えば割り算の余りを使って同値類を作ることができます。ある自然数\(n\in \mathbb{N}\)を３で割った余り\(n \mod 3\)を考えると、これは
\(0,1,2\)のいずれかになります。余り\(n \mod 3 =0\)となる自然数は\(0,3,6,9,12,….\)となりますが、これらを余り0という点で同一視することができます：\([0]=0,3,6,9,12,..\)。余り1,2のときも同様に\([1]=1,4,7,10,13,….\)、\([2]=2,5,8,11,14,….\)とできます。したがって自然数全体は\(\mathbb{N} =[0]\cup [1]\cup [2]\)と分類することができます。直感的には当たり前かもしれませんが、これが3で割った余りで同値類を作ることになります。同値類について少しイメージできたでしょうか。

以上集合論の関係について、お話しました。これらを使って、オブジェクト指向の話をしていきます。

2)オブジェクト指向と集合論

まずオブジェクト指向のオブジェクトですが、システム化する対象全般のことをいいます。なんかひどく抽象的な言い回しですが、そうせざるを得ません。なぜならシステム化するモノないしコトすべてに対して成立させるものなので、抽象的にしないと適用範囲が限られてしまうからです。

こういう抽象的な事柄を扱う論理体系は数学と相性がいいです。特に集合論は現代数学の全ての分野で基礎となっている分野なので、抽象度が非常に高いです。(だから汎用性も高い。)

オブジェクト全てを集めてきた集合を\(M\)とします。\(M\)が空集合だと、オブジェクトは存在しないことになり、それで終了となるので、\(M\)は空でない集合とします。

\(M\)に何かしらの同値関係\(\sim\)が与えられたとします。すると上の議論から、\(\sim\)による同値類が定義できます。この同値類ないしクラスが、オブジェクト指向における「クラス」と同じ意味になります。クラスの元を「インスタンス」とよびます。

したがってオブジェクト指向プログラミングにおいて、新しいクラスを定義することは、新しい同値関係を決めることと等価になります。

このあたり、巷の本だと初心者になんとかわかってもらおうと、ふんだんに例を用いて説明しているのですが、例が多すぎて、逆に本質がなかなかわかりづらかったりします。例を用いて説明することは重要ですが、最後に抽象度をあげて説明することも必要かと思います。本来オブジェクト指向自体が抽象度の高い話だからです。

さて、オブジェクト指向モデリングに、クラスに対して特化や汎化という概念がありました。これは集合論的には同値類の部分集合をとったり上位集合を考えたりすることにあたります。

ある同値類\([a]\)に、さらにある同値関係\(\sim ‘\)を追加するとします。
\[
[x_1]=\{m\in M \mid m\sim a \ \& \ m\sim ‘ x_1\}
\]
このとき同値類\([x_1]\)は\([a]\)の部分集合となりますが、これを特化といいます。\([x_1]\)は\([a]\)を継承したクラスとも言います。

逆に、まず\([x_1]\)があってそこから同値関係を削除して、大きな同値類を得ることを汎化といいます。上の例でいうと\([a]\)は\([x_1]\)の親クラス(基底クラス)とも言います。

簡単な図でいうと以下のイメージです。

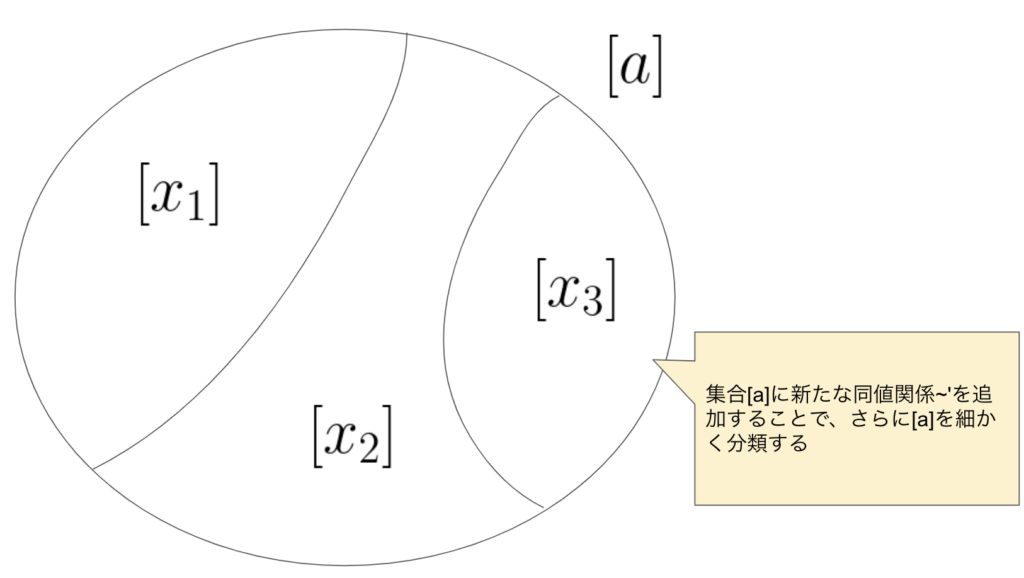
\([x_i],i=1,2,3\)は元々\([a]\)の部分集合でしたので、\([a]\)の同値関係は引き継いでいることになります。\([x_i],i=1,2,3\)は\([a]\)を継承しており、\([a]\)は\([x_i],i=1,2,3\)の汎化である、と言えます。

本日はここまでにします。

最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問い合わせにてよろしくおねがいいたします。