今回も前回に引き続き集合論の「関係」を用いてオブジェクト指向モデリングを整理していきたいと思います。
1)概念
オブジェクト指向モデリングでは「概念」という用語が出てきます。オブジェクト指向で非常に重要な用語なのですが、これが巷の書籍を見るとこの説明がまた非常にわかりにくいと(個人的に)感じます。
「概念はエンティティ、つまり実体のことであり、実体化したものがインスタンスとなる。そのためオブジェクト指向のプログラミング言語ではインスタンス化して初めて処理ができる。…」
、、、非常にわかりにくいです。少なくとも私は全くわかりませんでした。
まず、ER図を提唱したピーター・チェン氏は、概念はエンティティセットであると言ってます。エンティティセットはエンティティの集合(セット)の意味で、
概念=エンティティの集合
である、という意味になります。「集合」ということが重要なのですが、DB最適化の方法論等に適用されるうちに「セット」が抜け落ちて、さらにエンティティを「実体」と訳されたため、難解になってしまった気がします。
集合論的に言えば、概念とは対象の集合に同値関係が定義された同値類(もしくはクラス)のことで、同値類の元をインスタンスといいます。
2)関連クラス
つぎに関連クラスです。これは集合論における「関係」に他ならないのですが、少し見ていきます。
例えば、集合\(A,B\)を
\[
A\equiv \{とある会社の社員全体の集合\} \\
B\equiv \{\mathrm{iPhone},\mathrm{Android},\mathrm{feature\ phone}\}
\]
とします。
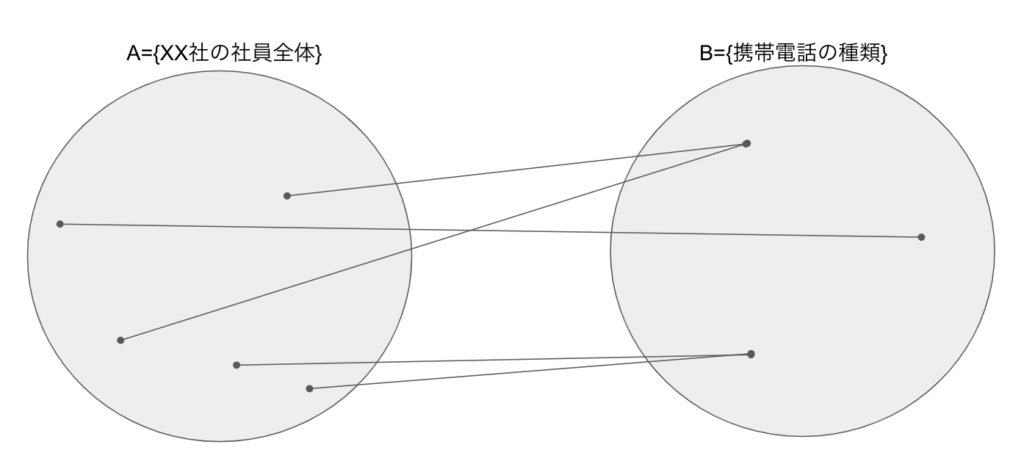
このとき社員がどの携帯電話をもっているかを考えます。これは集合\(A,B\)の部分集合を選ぶ、つまり関係を定義することになります:
\[
A\times B\ni a\times b \subset R 。
\]
例えば\( (X,\mathrm{iPhone} )\)は\(X\)さんはiPhoneを持つ、という意味になり、\( (\{Y,Z\},\mathrm{Android}) \)は\(Y\)さん,\(Z\)さんはAndroidをもつ、という意味になります。
さらに\(A\times B\)の部分集合の選び方は無数に存在しますが、選び方にある同値関係を入れることが出来ます。つまり1つ1つの関係を元とする集合を考え、その集合に同値関係をいれ同値類を作ることができることになります。この同値類が「関連クラス」になる、という形です。
上の例では関係\(R\)を「携帯電話所有」のような名前の関連クラスを定義することができます。
3)ロール
\(A,B\)を集合として、その関係\(A\times B\ni a\times b \subset R\)における\((a,b)\)をロールといいます。すなわち「関係」によって選ばれた部分集合のことです。上の例でいえば、例えば\(\{a,\mathrm{iPhone}\}\)とすれば、\(a\)は社員であると同時にiPhoneの所有者であることになり、iPhoneを所有物であることになります。
別の例で見てみます。例えば、集合Aを
\[
A=\{バーダック,孫悟空,孫悟飯,孫悟天\}
\]
としてみます。この集合\(A\)に親子という関係\(R\subset A\times A\)を入れます。\(R=(バーダック,孫悟空)\)と選ぶとこれは親子関係であり、バーダック:親、孫悟空:子というロールが定義されます。一方\(R=(孫悟空、孫悟飯)\)とすると、孫悟空:親、孫悟飯:子というロールになります。
つまりロールは関係に依存して定義されるもので、集合の同値類にはなり得ない、つまりクラスにはなり得ないことになります。
実際のシステム開発では、システム化を考える上で、上記の親子関係とは異なりロールが変化しないことが多々あり、ゆえ近似的にロールを同値類とみなして概念モデルを定義することも多いです。が、べき論ではシステムの変更容易性や拡張性が損なわれるためロールはクラスにしないのが無難です。
4)カテゴリー化
カテゴリー化です。これは集合論的に言えば、新しい同値関係を入れるに相当します。
先ほどと同様、集合\(A\)を\(A=\{とある会社の社員全体の集合\}\)とします。この集合\(A\)を役職という同値関係を定義して分類するとします。すると
\[
[a_1]\equiv\{a \sim 一般\}\\
[a_2]\equiv\{a \sim 課長\}\\
[a_3]\equiv\{a \sim 部長\}\\
[a_4]\equiv\{a \sim 本部長\}\\
[a_5]\equiv\{a \sim 取締役\}
\]
とできます。さらに
\[
A = \bigcup_{i=1}^{5}[a_i]
\]
とできます。
この集合\(A\)に別の観点、例えば役職はどうでもよく、単に所持しているケータイの種類\(B=\{\mathrm{iPhone},\mathrm{Android},\mathrm{feature\ phone}\}\)で分類したいとします。このとき
\[
[b_1]\equiv \{a \sim_B iPhone\}\\
[b_2]\equiv \{a \sim_B Android\}\\
[b_3]\equiv \{a \sim_B feature phone\}
\]
とでき、
\[
A = \bigcup_{i=1}^{3}[b_i]
\]
が成り立ちます。
同値類\([b_i]\)のように、集合に新たな同値関係を入れて分類することがカテゴリー化の定義になります。
このように集合論を用いて整理することで、オブジェクト指向モデリングを整理することが可能となります。オブジェクト指向モデリングは数学的基盤がないと言われていますが、よくよく検討してみると集合論に根ざした論理体系であるとみなすこともできます。
本日はここまでにします。
最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問い合わせにてよろしくおねがいいたします。