サラリーマンが確率論を勝手に解説する無謀な記事３

こんにちは、本日は確率分布の収束について、紹介します。
本稿はここで紹介した大数学者伊藤清氏の確率論等を参考にしてます。

1)背景

確率分布の列$\{\nu_n\}_n$が$\mu$に収束するとは、任意の有界な連続関数$f$に対して、 $$\int_{\mathbb{R}} f(x)\nu_n(dx) \rightarrow \int_{\mathbb{R}} f(x)\mu(dx)$$ となることを言いますが、この収束について突っ込んで勝手に解説するのが、本項になります。

2)本題

収束を定義するには、集合と位相を用意する必要があり、それらを定義していきます。

可測空間$(\mathbb{R},B(\mathbb{R}))$上の確率分布すべて集めてきた集合を$\mathbb{P}$とします。$\mathbb{R}$上の連続関数を$C(\mathbb{R})$とし、$f \in C(\mathbb{R}),\mu\in \mathbb{P}$に対して、 $$\langle f,\mu\rangle \equiv \int_{\mathbb{R}} f(x) \mu (dx)$$ とおきます。
$\langle f,\mu\rangle$ は厳密な内積ではないですが、あたかも内積にように扱うことができます。というのも、$C(\mathbb{R}),\mathbb{P}$はヒルベルト空間ではないものの、$C(\mathbb{R})$の共役空間は$\mathbb{P}$となり、双線型形式を定義できるためです。このあたりはこちらも参照してみてください。

さて、$\mathbb{P}$に位相を入れます。$\forall f\in C(\mathbb{R})$に対して、$n\rightarrow \infty$のとき $$\left| \langle f, \nu_n-\mu \rangle \right|= \left| \int_{\mathbb{R}} f(x) \nu_n (dx)-\int_{\mathbb{R}} f(x) \mu (dx) \right| \rightarrow 0$$ とするような位相です。この位相による$\mu$の近傍は $$U(\mu,\varepsilon) = \left\{ \nu \in \mathbb{P} \mid \left| \langle f, \nu-\mu \rangle \right| < \varepsilon ,\ \forall f\in C(\mathbb{R})\right\}$$ で与えられ、関数解析の言葉で弱位相といいます。

この弱位相はある距離$\rho$によっても与えることができます。$C(\mathbb{R})$の部分集合でコンパクトな台をもつ連続関数の全体を$C_K$とすると、$C_K$は可分になることが知られていますので、可算な稠密部分集合をもつことになります。それを$\{ g_n\}_{n\in \mathbb{N}}$とすると、 $$\rho(\mu,\nu) \equiv \sum_{n=1}^{\infty}2^{-n} \min \left\{ \left| \langle g_n,\mu\rangle – \langle g_n,\nu\rangle \right|,1 \right\}$$ は距離となります。

さて、距離空間$(\mathbb{P},\rho )$における収束を考えたいのですが、残念ながら$(\mathbb{P},\rho )$は完備でない空間となるため、すこし位相に関して工夫する必要が出てきます。それを以下のように行います。(これをレビィ距離といいます。)

まず分布$\mu$の分布関数を $$F(x) = \mu(-\infty , x]$$ で定義します。一般に$y=F(x)$は不連続ですが、不連続な点を縦線でつなげば、連続なグラフになります。$y=F(x)$と$y=-x +t$の交点は２つ存在しますが、それらの距離を$G(t)$とします。

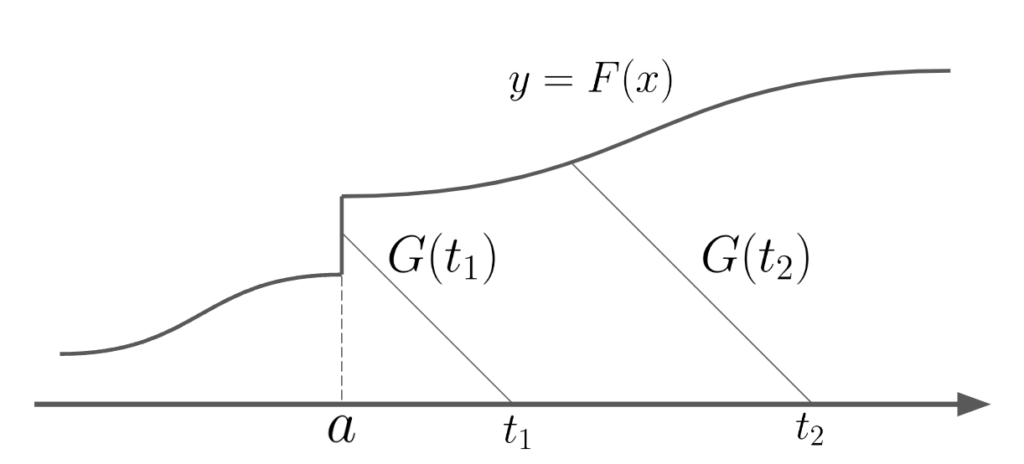
関数$G(t)$は単調増加関数で $$|G(t)-G(s)| \leq |t-s| \\ \lim_{t\rightarrow -\infty}G(t)=0, \lim_{t\rightarrow \infty}G(t)=\sqrt{2}$$ をみたすことはすぐわかります。この関数の全体を$\mathbb{G}$とすれば、この$\mathbb{G}$は$\mathbb{P}$の間に1対1に対応することになります。$\mathbb{G}$の距離を $$d(G_1,G_2)=\sup_t |G_1(t)-G_2(t) |$$ とし、 $$d_G(\mu,\nu)=d(G_{\mu},G_{\nu})$$ で定義すると、距離空間$(\mathbb{P},d_G)$は完備距離空間になります。

したがって、確率分布の空間が完備距離空間になるので、収束を定義できるようになります。

3)その他

確率分布$\{\nu_n\}_n,\ \mu$の確率変数を$\{X_n\}_n,\ X$とします。いま分布列$\{\nu_n\}_n$が$\mu$に収束するとき、確率変数$\{X_n\}_n$は$X$に「法則収束」するといいます。

確率変数は、法則収束以外にも様々な収束を考えることができるのですが、それは別途解説したいと思います。

なお確率分布全体の集合$\mathbb{P}$を多様体とみて、その幾何学的な性質を調べるのが「情報幾何学」となります。情報幾何は統計的推論や機械学習、統計力学など様々な分野に応用されており、最近情報幾何学の専門雑誌が刊行されるくらい活発な分野です。ちゃんと扱うには現代微分幾何学の知識が必要なため、こちらも別途勝手に解説していきたいと思います。

最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問い合わせにてよろしくおねがいいたします。