今回は現代物理学について
- 大学以降の物理はどんな内容を勉強するのか。
- 現代物理学の分野ってどんなことがあるのか
について、私の分かる範囲で説明していきます。
現代物理学は非常に範囲が広く、枚挙にいとまがないのですが、独断と偏見で無理やり1枚にまとめると以下になります。
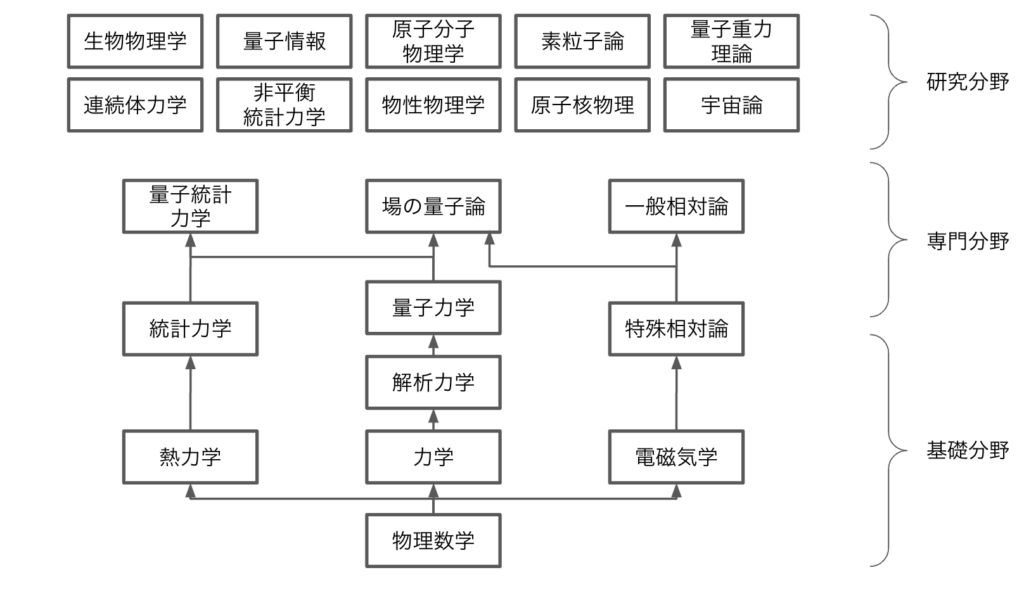
- 「基礎分野」と言っても簡単であると意味ではありません。基礎といっても「Basic」ではなくて「Foundation」の方が意味合いとしては近いです。
- 図中の矢印はあくまで目安です。最も影響の大きい分野をつないでいるだけとなります。例えば、統計力学を学ぶのに、力学や電磁気学が全く必要ないかと言われるとそうではありません。統計力学はミクロな粒子たちに力学や電磁気学の法則に従っていると仮定して、統計処理をしてマクロな状態を導いていくからです。また特殊相対論を学ぶのに力学が必要ない、ということでもないのです。
- また図中の上段の「研究分野」は基本的にいろいろな専門分野の知識が前提となっているため、矢印は記載してません。
以下それぞれの分野を少し解説してきましょう。
- 物理数学
物理学は数学の「ことば」で記述されているので、その「ことば」をまずは学びます。「ことば」は使えるようになることが重要ですので、物理数学は数学的に厳密な理論展開はせず、正しい結果が得られればよい、というスタンスで学習します。(広範囲なので、とてもじゃないがやりきれない。)
例、微分積分、線形代数、ベクトル解析、常微分方程式、偏微分方程式、変分法、関数論(複素解析)、フーリエ/ラプラス変換、群論 etc. - 力学
その名の通り力学です。高校物理にもこの分野があるのでイメージしやすいかと思いますが、物理学科の力学では、微分方程式を駆使して運動方程式を立て、ゴリゴリ計算していきます。
物理学では、現象を数式でモデル化し、また数式から現象をイメージすることが重要なスキルとなりますが、その最初の練習となります。
角運動量や剛体の運動もここで初めて扱うようになります。 - 解析力学
力学を数学的に洗練させた分野です。力学で扱う運動方程式\(F = ma\)は座標の選び方によっては、計算がえぐいことになりますが、それを解決するのが解析力学です。
また変分原理という、この世界の物体の運動は「作用」を最小にする経路をとって運動する、という考え方が登場し、これはすべての物理学分野でも適用されるとても重要な原理となってます。
この「作用」を定義する上でラグランジアン、ハミルトニアンという概念も初めて出てきます。
ラグランジュの未定乗数法は「作用」を最小化する上で発見された手法ですが、現在は物理学の枠を超えて、制御工学や経済学でも応用されています。
のちに出てくる量子力学はこの解析力学の一般化座標/一般化運動量やポワソン括弧という概念を演算子や交換関係という概念に置き換えて構築されますので、そういう点でも重要です。
ちなみにモーペルチューイは最小作用の原理を通じて、神の存在を示そうとしたらしく、それくらい普遍的な原理です。 - 熱力学
熱力学です。高校物理でもあった分野ですが、大学の物理ではエントロピーという概念が出てくるのが大きな違いです。熱力学はエントロピーの概念をもって初めて完全な理論となりえる(と勝手に思ってます)。
熱力学は他の分野からみると少し掠れて見えるかもしれないが、そんなことはなく、場の理論や相対論といった現代物理学が出てきても何も変更を受けなかった盤石な理論体系です。
むしろ最近はブラックホールにも熱力学を適用して、エネルギーを出して蒸発することを示していたりして最先端の研究でも使われています。
様々な熱力学量が登場し、偏微分が活躍します。 - 電磁気学
最初の難関分野です。高校の電磁気と違い、ベクトル解析という、ベクトルの微積分のことばで記述されています。これは電場や磁場といった「場」という概念が登場し、これを数学的に扱うためにベクトル解析の知識が必要となるのです。
ガウスの法則やファラデーの法則、変位電流など電磁気学で発見された様々な法則は、最終的にMaxwell方程式にまとめられます。電気と磁気という別々の対象と扱っていたものが、一つの基本法則にまとめられていく過程を追体験できる最初の分野かと思います。
高校物理で光は電磁波である、という事実を習ったかと思いますが、これをMaxwell方程式を解いて証明したりします。
ちなみに特殊相対論を構築するモチベーションとなったのも電磁気学からになります。
今回はここまでにします。もしよろしければ以下の記事もご覧ください。
- 現代物理学への招待1 ー物理数学、力学、熱力学、電磁気学ー ※本稿
- 現代物理学への招待2 ー量子力学、統計力学、特殊相対論ー
- 現代物理学への招待3 ー場の量子論、量子統計力学、一般相対論ー
- 現代物理学への招待4 ー素粒子論、量子重力理論、宇宙論ー
- 現代物理学への招待5 ー原子核物理、原子分子物理、物性物理ー
- 現代物理学への招待6 ー量子情報、非平衡統計力学、生物物理、連続体力学ー
最後まで読んでくださりありがとうございます。
質問等はコメント欄かお問い合せにてよろしくおねがいいたします。
「現代物理学への招待1」への4件のフィードバック
コメントは受け付けていません。