前回エニオンとはなんぞや?の部分について、言及しましたが、本稿はエニオンをどうやって操作するかについて解説していきます。
今回もこちらをもとにしてます。
※今回の内容も前回同様深入りすると位相的場の量子論の知識が必要となり私の理解の範囲を超えるので、ざっくりした記述になってます。
1)フュージョン則
エニオン全体を
\[
M=\{ 1,a,b,c,…..\}
\]
というようにラベルします。これらはちょうどトポロジカル不変量に相当します。\(1\ \)はエニオンが存在しないことを表すラベルです。
位相的場の量子論(TQFT)によると、一般にエニオンの合成は「フュージョン則」と呼ばれる、
\[
a\times b =\sum_{c\in M }N_{ab}^c c
\]
に従います。ここで、\(N_{ab}^c\)はフュージョン係数で、\(N_{ab}^c=0,1,..\)といった非負整数に値を取ります。例えば\(a\times a = 1 + b\)となる場合、\(a\)2つのフュージョンの結果、真空になる、もしくは粒子\(b\)に変わることを意味しています。
右辺\(\sum_{c\in M} N_{ab}^c c \)が単項である場合、可換エニオンに相当し、そうでない場合非可換エニオンに相当します。
フュージョンの自由度はその結果によって張られる状態空間となるので、\(a,b\)をフュージョンして\(c\)が生成される状態を
\[
|ab;c\rangle
\]
と表すことにします。正規直交条件として
\[
\langle ab;c|ab;d\rangle =\delta_{cd}
\]
が成り立ちします。この状態空間を「フュージョン空間」と呼びます。
フュージョンの仕方が\(N\)通りある場合、フュージョン空間は\(N\)重に縮退した状態空間になります。前回の投稿でエニオンの基底状態と励起状態にはエネルギーギャップが存在することに触れましたが、フュージョン空間は非局所的な操作によって張られており、ノイズなどの局所的な摂動によってエネルギーギャップを超えることがなく、安定した状態であると言えます。
次にエニオン3つをフュージョンする場合を考えます。\(a,b,c\)のエニオンがフュージョンして最終的に\(d\)になると仮定します。まず\(a,b\)がフュージョンして\(e\)ができ、\(e,c\)がフュージョンして\(d\)となるような操作を
\[
|(ab)c;ec;d\rangle
\]
と表します。他方、先に\(b,c\)がフュージョンするケースも考えられますので、
\[
|a(bc);af;d\rangle
\]
という状態も考えられます。これらの状態間を行き来する演算子を\(F-\)行列といい、
\[
|(ab)c;ec;d\rangle = \sum_{f\in M}\left(F_{abc}^d \right)_{ef} | a(bc);af;d\rangle
\]
という関係性が存在します。\(\left(F_{abc}^d \right)_{ef}\)は演算子\(F_{abc}^d\)の行列表現で、和はエニオン\(b,c\)のフュージョンの結果分、すなわち\(N_{bc}^f\ne 0\)となる分だけとります。これらを図式にまとめると以下になります。
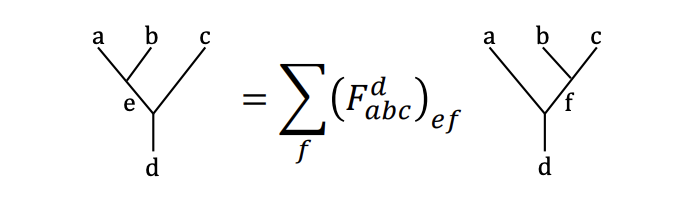
※こちらのp15より抜粋
2)交換演算子
\(a,b\)を交換した状態\(|(ba)c;ec;d\rangle\)を考えていきます。
前回の投稿で、可換エニオンの交換演算子は
\[
R = \left\{\begin{matrix} e^{i\theta}&:\mathrm{Abelian}\\ U&:\mathrm{non-Abelian} \end{matrix}\right.
\]
と表しました。
ここでHexagon方程式という式を解くと、\(R\)の行列表現\(R_{ab}^f\)を求めることができるようです。
\(|(ab)c;ec;d\rangle\)を初期状態として、時計回りに\(a,b\)を交換した場合、
\[
|(ba)c;ec;d\rangle = \sum_{f\in M}R_{ab}^f \delta_{e,f} | (ab)c;ec;d\rangle
\]
となります。
\(|(ab)c;ec;d\rangle\)を初期状態として、時計回りに\(b,c\)を交換する場合、やや複雑になり以下の数式になります。
\[
|(ac)b;ec;d\rangle = \left(F_{abc}^d\right)^{-1} R \left( F_{abc}^d\right) | (ab)c;ec;d\rangle
\]
まず\(| (ab)c;ec;d\rangle\)に\(F_{abc}^d\)を作用させて、\(|a(bc);af;d\rangle\)とします。その後交換演算子\(\ R = (R_{bc}^f)\)を作用させて、\(| a(cb);af;d\rangle\)が得られ、最後に \( \left(F_{abc}^d\right)^{-1}\)を作用させて、\(|(ac)b;ec;d\rangle\)が得られます。これらの図式にすると以下になります。
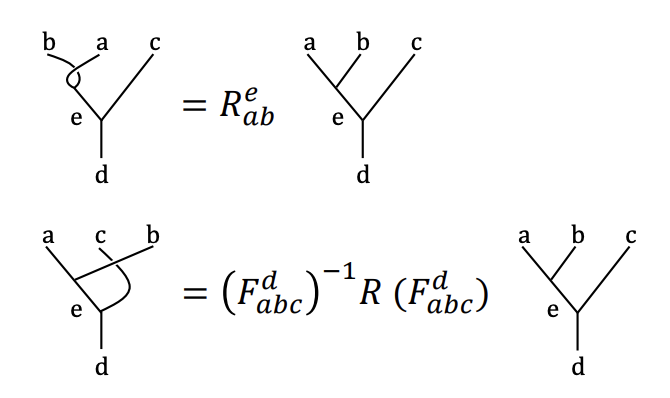
※図はこちらのp16から抜粋
以上がエニオン操作の一般論で、要約すると
・フュージョン係数\(N_{ab}^c\)はエニオンの数やフュージョンの仕方を表し、
・\(F\)行列\(F_{ab}^c\)は、フュージョン空間の構造を記述し、
・交換演算子\(R\)はエニオンの交換を表す。
というようなイメージとなります。
3)イジングエニオン
さて1)、2)を満たすようなエニオンはいくつか知られており、
・フィボナッチエニオン(Fibonacci Anyon)
・イジングエニオン(Ising Anyon)
が挙げられますが、ここではイジングエニオンを詳しくみていきます。
イジングエニオンモデルでは、フェルミオン\(\ \psi \ \)とエニオン\(\ \sigma \ \)からなる系になり、フュージョン則は
\[
1\times 1 = 1,\ 1\times \psi = \psi, \ 1\times \sigma = \sigma \\
\psi\times \psi = 1,\ \psi\times \sigma = \sigma \\
\sigma \times \sigma = 1 + \psi
\]
となります。少し補足すると、\(\psi\times \psi = 1\ \)は2つのフェルミオンが揃うと何もない真空のように振る舞い、\( \psi\times \sigma = \sigma \)は フェルミオンとエニオンが合わさると単体のエニオンのように振る舞う、ということを意味しています。最後の式\( \ \sigma \times \sigma = 1 + \psi\ \)が非可換エニオンの特徴で、エニオン2つがフュージョンすると、真空or1つのフェルミオンのように振る舞います。
エニオン3つのフュージョン則は
\[
\sigma\times \sigma \times \sigma
= \sigma\times (1+\psi) \\
=\sigma\times 1 + \sigma\times \psi \\
=2\sigma
\]
となるので、このときのフュージョン空間は
\[
\left\{ |(\sigma\sigma)\sigma;1\sigma;\sigma\rangle,
|(\sigma\sigma)\sigma;\psi\sigma;\sigma\rangle \right\}
\]
となります。このときF-行列\(F_{\sigma\sigma\sigma}^{\sigma}\)は
\[
F_{\sigma\sigma\sigma}^{\sigma} = \frac{1}{\sqrt{2}}\begin{pmatrix}
1 & 1 \\
1 & -1 \\
\end{pmatrix}
\]
で与えられます。このとき交換演算子\(\ R\ \) は
\[
R=\begin{pmatrix}
R_{\sigma\sigma}^1 & 0 \\
0 & R_{\sigma\sigma}^{\psi} \\
\end{pmatrix}
=e^{i\pi/8}
\begin{pmatrix}
1 & 0 \\
0 & e^{i\pi/2} \\
\end{pmatrix}
\]
で与えられます。したがって、ちょっとした計算の結果、
\[
F^{-1}R^2F = e^{i\pi/4}\begin{pmatrix}
0 &1 \\
1 & 0 \\
\end{pmatrix}
\]
となることがわかります。これがベリー位相に関連していることは前回の記事の通りです。
次回からエニオンモデルをつかって、量子ビットを構成していきます。
最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問合せにてよろしくおねがいいたします。
「量子コンピュータを勝手に解説する記事 トポロジカル量子計算について2」への1件のフィードバック