数学Ⅲを使った高校物理４

今回は交流回路について解説したいと思います。

高校物理の交流回路の問題で、

1. 交流電源とコイル
2. 交流電源とコンデンサー

を繋いだ時の電流の位相差の公式がありましたが、これを数学Ⅲを使って導いてみます。

0)交流電源と抵抗

その前にまず抵抗のみ繋いだ場合を考えてみましょう。

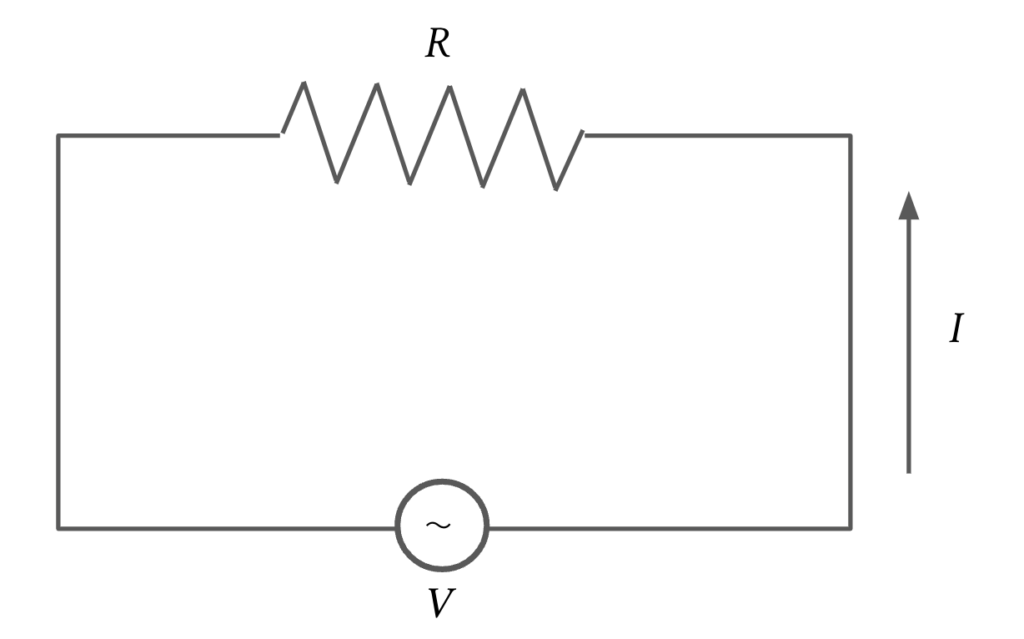
交流電源はsin波、\(V =V_0\sin\omega t\)とします。反時計回りを正として、キルヒホッフの法則(=閉回路の電位差はゼロ)を用います。抵抗\(R\)に電流\(I\)が流れた時の電圧降下はオームの法則から\(IR\)でしたので、

\[V-IR = 0\]

が成り立ちます。したがって、

\[V_0\sin\omega t – IR=0 \Rightarrow I = \frac{V_0}{R}\sin\omega t\]

となります。すなわち電圧と電流の位相差は等しくなることがわかります。

1)交流電源とコイル

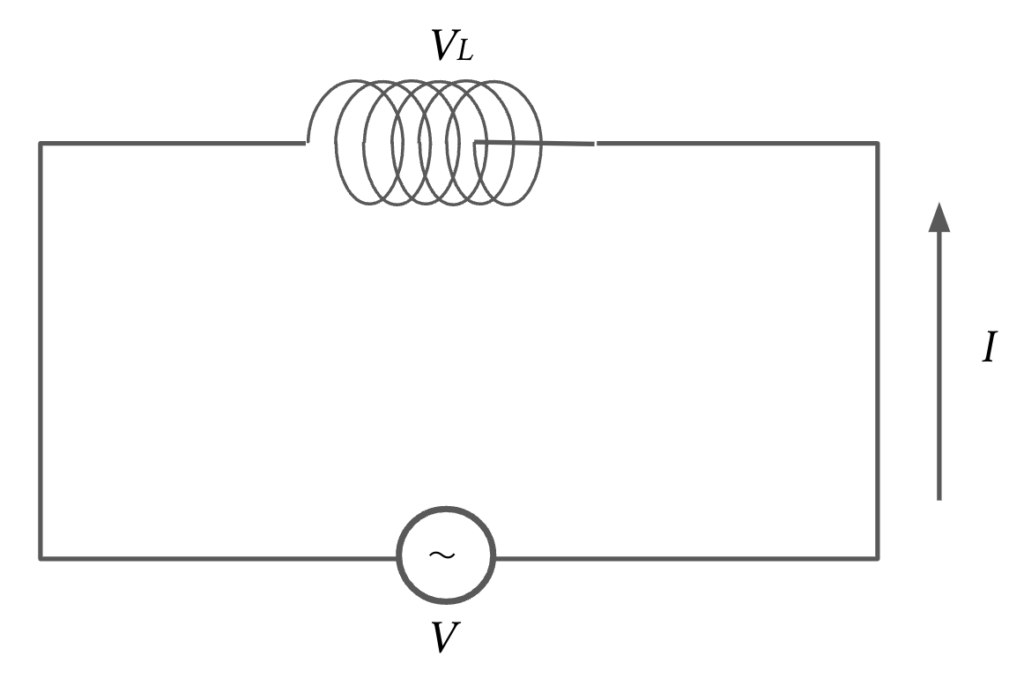
抵抗の場合と同様、交流電源はsin波、\(V =V_0\sin\omega t\)とします。反時計回りを正とします。

電流Iが流れている時のコイルの電位差\(V_L\)は

\[V_L = -L\frac{\Delta I}{\Delta t}\rightarrow -L\frac{dI}{dt} \ \ \ (\Delta t \rightarrow 0) \]

となりますので、キルヒホッフ則より

\[V_0\sin\omega t -L\frac{dI}{dt}= 0 \Rightarrow \frac{dI}{dt}= \frac{V_0}{L}\sin\omega t\]

となります。電流Iの形を知りたいので、時間tで積分を実行します。数学IIIの知識、\(\int \sin x dx = -\cos x+C\)、\(\int f(ax+b)dx = F(ax+b)/a +C\)、(\(F(x)\)は\(f(x)\)の原始関数、Cは積分定数)を使うと

\[I= -\frac{V_0}{L\omega}\cos\omega t + C \]

となりますが、積分定数Cを決める必要があります。
これは1周期をTとして、\([s,s+T]\)で積分とするとゼロになるという交流条件

\[\frac{1}{T}\int_{s}^{s+T}I(t) dt =0\]

から

\[
\frac{1}{T}\int_{s}^{s+T}I(t) dt = \frac{1}{T}\int_{s}^{s+T}\left(-\frac{V_0}{L\omega}\cos\omega t + C \right)dt =\frac{1}{T}\left[-\frac{V_0}{L\omega^2}\sin\omega t + Ct \right]_{s}^{s+T} \\
=\frac{1}{T}\left(-\frac{V_0}{L\omega^2}\bigg(\sin\omega\left(s+T\right)-\sin\omega s \bigg)+C(s+T)-Cs \right)
\]

三角関数の和積の公式\(\sin x-\sin y = 2\cos(x+y)/2\sin(x-y)/2\)を用いて計算を進めていくと

\[
=\frac{1}{T}\left(-\frac{2V_0}{L\omega^2}\cos(2\omega s + \omega T)\sin\frac{\omega T}{2} +CT \right) \tag{1}
\]

ここでTは1周期を表す時定数だったので、\(\sin\omega T/2 = \sin \pi =0\)。ゆえに、(1)の第１項 = 0。
またTの定義から\(T\neq 0\)であるので、結果として、\(C=0\)となります。

以上から電流は

\[I(t) = -\frac{V_0}{L\omega}\cos \omega t\]

となる。これをsinで表すと

\[I(t) = \frac{V_0}{L\omega} \sin\left(\omega t – \frac{\pi}{2}\right)\]

となります。数学Ⅰで出てきたように、\(y=f(x)\)を右へ\(a\)だけ平行移動すると\(y=f(x-a)\)となるのでした。これを使うと位相に着目すれば電圧を\(\pi/2\)右へ平行移動すると電流に一致することになりますので、電流は電圧にくらべ位相が\(\pi/2 \)だけ遅れることになります。

今回積分定数Cについて、数学IIIまでの数学を使って厳密に求めてみました。
この背景には、境界条件のもと微分方程式を解くことに繋がっていくのですが、完全に高校数学/高校物理の範囲を超えるので、別の記事で書いていきたいと思います。

交流とコンデンサーの関係については、次回に記事にて記載していきます。

最後まで読んでくださりありがとうございます。
質問等はコメント欄かお問い合わせよりよろしくおねがいいたします。