さて、本日は前回までに定義した、測度と可測関数の概念を用いて、積分を定義していきます。
\((\Omega,\mathcal{F},\mu)\)を測度空間、\(f:\Omega \rightarrow X\)を可測写像とします。いままで同様、\(\Omega=[0,1]\)ととります。
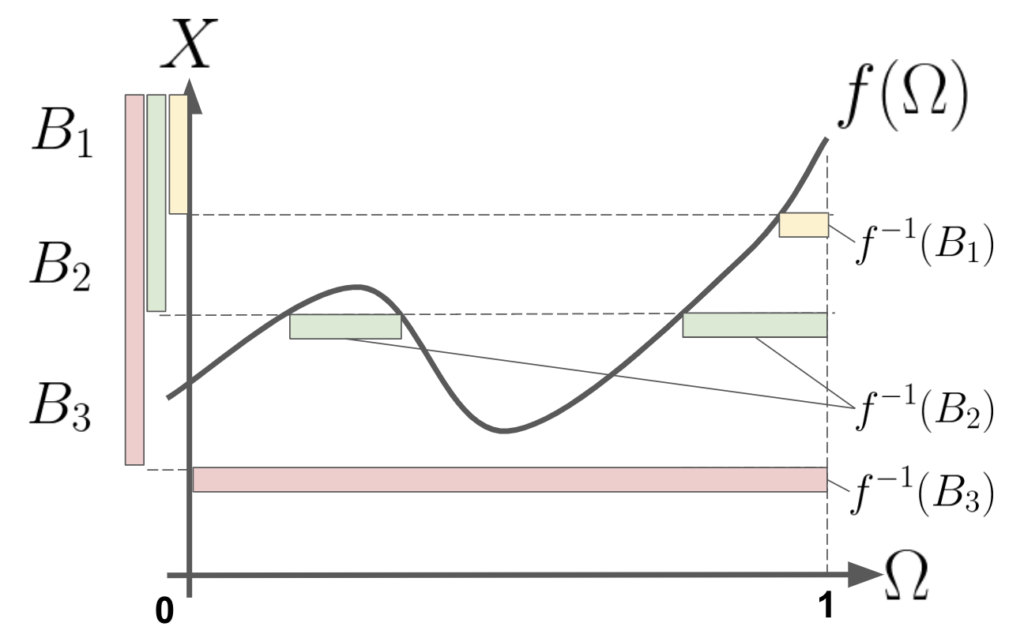
上の図はこちらの図2と本質は同じです。横軸に\(\Omega\)、縦軸に\(X\)をおいて、\(f\)をグラフで表したものになります。
\(f\)は可測関数でしたから、\(X\)上の全ての区間は\(\Omega\)上でも区間になります。ただし今回は\(X\)上の区間を\(B_i = [b_i,\infty),i=1,2,….\)という形でとってます。
さて、上記関係性を用いて、面積、つまり積分を求める方法を考えます。\(f^{-1}(B_i)\)が\(\Omega\)上の区間でしたので、横の長さは\(\mu(f^{-1}(B_i))\)とできます。これに縦の長さをかければ、横に細長い棒の面積が求まります。
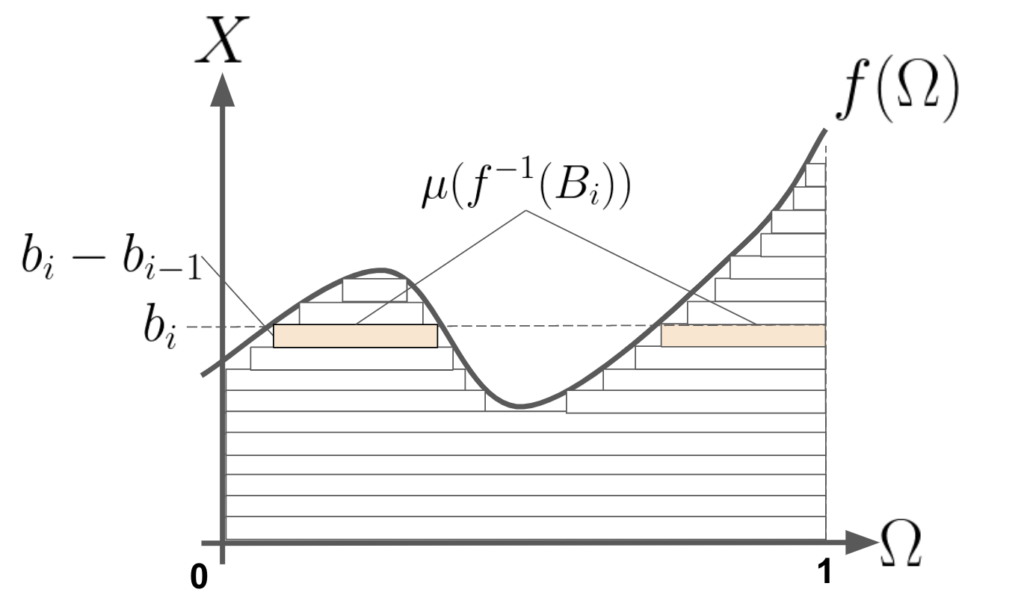
1つの長方形の面積 = \((b_i-b_{i-1})\times \mu(f^{-1}(B_i))\)
といった感じですね。したがって面積\(S\)は、\(b_i-b_{i-1}\equiv \Delta b\)とすれば
\[
S\sim \sum_{i}\mu(f^{-1}(B_i))\Delta b
\]
とできます。あとは\(\Delta b \rightarrow 0\)という極限をとればよく
\[
S=\lim_{\Delta b \rightarrow 0} \sum_{i} \mu(f^{-1}(B_i))\Delta b = \int \mu(f^{-1}(B))db \equiv \int f d\mu
\]
となります。これがよくある「ルベーグ積分は横に切って足し合わせる」一般的な説明になります。これはこれでいいのですが、ルベーグ積分の定義から見ると少し離れている感が否めないと個人的には思ってしまいます。それを説明するためにルベーグ積分を厳密に定義していきます。
まず指標関数を定義します。
DEF.4 指標関数
\(A\)を空でない集合とする。写像\(\chi\)を\(\chi :\mathcal{F}\times X\ni A \times x \rightarrow \chi_{A}(x) \in \{0,1\}\)、
\[\chi_A(x) = \left\{\begin{matrix} 1 & x \in A \\ 0 & x \notin A \end{matrix}\right. \]
と表させる関数を指標関数(もしくは指示関数,特性関数)という。
\(A\)を固定すれば、指標関数は可測関数であることがわかります。
次に単関数を定義します。
DEF.5 単関数
\((X,\mathcal{F},\mu)\)を測度空間とする。\(A_1,A_2,…,A_n\in \mathcal{F}\)と実数\(a_1,a_2,…,a_n\)に対して、
\[
f_n(x) = \sum_{i=1}^n a_i\chi_{A_i}(x)
\]
とできるような関数\(f_n\)を単関数とよぶ。
つまり単関数は指標関数の線型結合となります。ゆえ、単関数も可測関数になります。さらに\(n\)を十分大きくとれば、任意の可測関数は単関数で近似できることが示せます。(証明は略)
最後にこれまでの知識を用いて積分を定義することができるようになります。
DEF.6 ルベーグ積分
\((X,\mathcal{F},\mu)\)を測度空間とし、\(f:X\rightarrow Y\)を可測関数とする。\(\{A_i\}_{i\in \mathbb{N}}\in\mathcal{F}\)に対して、\(f(x) = \sum_i^\infty a_i\chi_{A_i}\)が成り立つとする。このとき
\[
\sum_i^{\infty} a_i\mu(A_i)
\]
が収束(絶対収束)するとき、これをルベーグ積分といい、\[\int f(x)d\mu(x) \ \ \mathrm{ or } \ \int f(x) \mu(dx)\]と表現する。
DEF.6をみると\(a_i\times \mu(A_i)\)を足し合わせてるのですが、これは実は縦が\(a_i\)で横が\(\mu(A_i)\)となる長方形です。

\(f_n\rightarrow f,n\rightarrow \infty\)となるので、実は縦に切って極限をとることになり、一瞬リーマン積分と同じに思えるかもしれません。リーマン積分は横軸は分割の極限であるのに対し、ルベーグ積分は測度になっているところが異なる点です。測度を用いることで、積分できる関数が格段に多くなります。
ルベーグ積分の表記についても少し触れておきます。個人的にはルベーグ積分の表記は\(\int f(x)\mu(dx)\)の方が、\(\int f(x)d\mu(x)\)よりもしっくりきます。というのも測度の定義域はあくまでσ加法族\(\mathcal{F}\) であるので、\(\mu\)の引数は可測集合となるはずです。\(x\)も\(dx\)も可測集合ではありますが、\(x\)と書くと一点の可算集合となり、\(dx\)と書けば感覚的に微小な幅を意味し、非可算集合になります。\(\mu(x)\)と書くと、可算集合の測度なので厳密に\(0\)となる一方、\(\mu(dx)\)は微小ではありますが\(0\)ではないので、足し合わせることが可能となり、つまり積分\(\int f(x)\mu(dx)\)が定義できるイメージになります。つまり点をいくら集めても線にならないが、微小な線を集めればそれは線になる、という感覚です。
とはいえ、\(dx\)の測度\(\mu(dx)\)は非常に小さいので、それを\(d\mu(x)\)で表すのは全く変ではないのですが、、なんというかもはや個人の趣味/趣向的なところの話なのでこれくらいにします。
本日はここまでにします。次回もう少しルベーグ積分と測度を深掘ってみます。
最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問い合わせにてよろしくおねがいいたします。
「サラリーマンが測度論を勝手に解説する無謀な記事3」への1件のフィードバック