こんにちは、\(\varepsilon\)-\(\delta\)について解説していきます。
まずは数列の極限からです。数列の場合は\(\varepsilon\)-\(N\)法とも呼ばれています。
数列の収束は
\[
\lim_{n\rightarrow\infty}a_n = a
\]
と書かれましたが、これを\(\varepsilon\)-\(N\)で表すと
\[
\forall \varepsilon >0,\exists N\in \mathbb{N}:\forall n >N \Rightarrow |a_n -a |< \varepsilon
\]
となります。同じことですが日本語で書くと、
「任意の\(\varepsilon > 0\)に対して、ある\(N\)が(\( \varepsilon\)に依存して)存在して、もし\(n >N\)ならば、\(|a_n-a| < \varepsilon\)が成り立つ。」
になります。もうすこし補足すると、「\(0\)より大きい、どんな数\(\varepsilon\)を持ってきても、それに対応する\(N\)があって、その\(N\)より大きい\(n\)だったら、収束値\(a\)と\(a_n\)とのずれは\(\varepsilon\)より小さくなる」という感じです。
これは初見だとクラクラしてくるかと思いますが、以下これの意味を解説します。
例えば
\[
a_n = \frac{n}{n+1},\ n\in\mathbb{N}
\]
となる数列を考えてみましょう。この数列は\(1/2,2/3,3/4,4/5….\)となる数列で\(n\rightarrow \infty\)で\(1\)に収束となる数列となります。
毎度拙い図ですみませんが、図であわらすと以下のようなイメージになります。
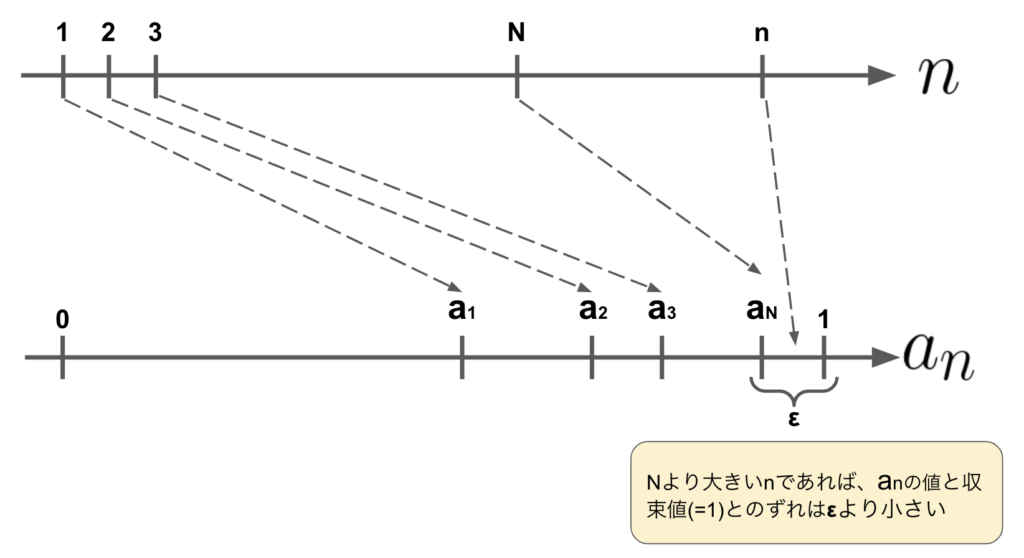
まず\(\varepsilon\)の値を決めます。これは収束値との誤差の値を意味で、要はこれくらいならずれててもいいという値です。英語で誤差をerrorと呼びますが、これは数学者コーシーによって、先頭のeをギリシア文字化して\(\varepsilon\)にしたのが始まりのようです。
今\(\varepsilon = 10^{-4}\)としてみます。とすると
\[
|a_n-a| < \varepsilon \Leftrightarrow \left| \frac{n}{n+1}-1 \right| < 10^{-4}
\]
となり、整理すると\(n>10^{4}-1\)となります。つまり\(N=10^{4}-1\)となり、\( \varepsilon = 10^{-4}\)に対して、\(N = 10^{4}-1\)がきまったことになります。
\(\varepsilon = 10^{-4}\)では、全然誤差の範囲じゃない、ということであれば、\(\varepsilon = 10^{-10}\)としてみましょう。とすると同様に計算して\(N=10^{10}-1\)が得られ、\(n>N=10^{10}-1\)ならば\( |a_n-1| < 10^{-10}\)が成り立つことがわかります。
それでも足りないということであれば、\( \varepsilon =10^{-10000000000} \)にしてみます。これも上記と同様に\(n > N=10^{10000000000}-1\)なら、\( |a_n-1| < \varepsilon\)が成り立ちます。
以上から、「\( 0\)より大きければ、どんな実数\(\varepsilon\)をもってきても、必ずその\( \varepsilon\)に対応する \(N\)が存在し、\(n>N\)に対して、\(|a_n -1| < \varepsilon \)になる」ことがわかります。
今回は数列\(a_n = n/(n+1)\)を例にしましたが、一般に具体的な\(N\)は数列によって変わります。これを見つけるのが\(\varepsilon\)-\(N\)法の証明方法のキモになります。
さて、実際に解析する場合ですと、収束先がわからない場合も多々あります。そんなときは収束するかどうかから吟味が必要になります。その吟味する際に使うのがコーシー列というものです。
数列\(a_n\)がコーシー列であるとは、\( \forall \varepsilon >0 \)に対して、\(\exists N \)が存在して、\(n,m > N \)だったら、\( |a_n-a_m|< \varepsilon \)が成り立つときをいいます。
まぁ端的に言って、収束値が\(a\)だったのを、十分大きい\(m\)での\(a_m\)にしただけになります。収束するのであれば、十分大きい\(n,m\)であれば、その差\(|a_n-a_m\)も十分小さくなるよというものです。
先ほどの
\[
a_n=\frac{n}{n+1}
\]
がコーシー列かどうかみてみます。
とりあえず\(\varepsilon = 10^{-10}\)程度に考えておきます。このとき\(m>n>N\)とすると
\[
\left|a_n-a_m\right|=\left|\frac{n}{n+1}-\frac{m}{m+1}\right| <\left|\frac{n}{n+1}-1\right|=\left| \frac{-1}{n+1}\right|<\frac{1}{n}
\]
となります。\(1/n\)は明らかに収束するので、\(\varepsilon\)に対して\(N\)が存在して、\(n>N\)ならば\(1/n<\varepsilon\)が成立します。したがって、
\[
\left|a_n-a_m\right| < \epsilon
\]
が成り立ちます。ゆえに\(a_n\)はコーシー列になります。
コーシー列を使うメリットは収束先が不明な場合も使える点です。実際に解析を行うとき収束先は未知の場合が多いです。そのときまず収束するか、発散するかを吟味する必要がありますが、そんなときに使われます。
収束先が不明なケースというのはかなり出てきます。実数や複素数に値をもつ数列であれば、あまり気にならないですが、関数を全て集めてできた集合上の数列、すなわち関数列を相手にすると、収束先が未知であることが多々あります。
収束先が不明な場合、万が一対象の空間からはみ出てしまう場合もあります。これは都合が悪く、はみ出ないようないい感じの性質を抽象化できないか、ということで考えられたものがこちらで定義した完備、という概念になります。
なお、はみ出るというのはどういうことかというと、例えば以下のような漸化式を見てみます。
\[
a_1 = \frac{3}{2},\ a_{n+1} = \frac{a_n^2+2}{2a_n}
\]
\( \{a_n\}_n \)は全ての\(n\in\mathbb{N}\)で有理数になりますが、この収束値は\(\sqrt{2}\)の無理数になり、有理数からはみ出てしまう、といった感じです。
ちなみに収束値が\(\sqrt{2}\)になる理由は、高校数学の範囲で十分示せます。
収束値を\(a\)とすれば、特性方程式から\(a = (a^2+2)/2a \Leftrightarrow a^2 =2\)で、\( a_n > 0\)であるから、\(a=\sqrt{2}\)。ゆえに、\[
a_{n+1}-\sqrt{2} = \frac{(a_n-\sqrt{2})^2}{2a_n}<\frac{a_n}{2a_n} (a_n-\sqrt{2})= \frac{1}{2} (a_n-\sqrt{2}) < \frac{1}{2^n}(a_1-\sqrt{2})\rightarrow 0 \ (n\rightarrow \infty)
\]
上記の方法で極限を扱う手法は、一般に\( \varepsilon\)-\( \delta \)と呼ばれていますが、これは数列に限らず、連続性や微分など極限を扱うもの全般で使われます。このあたりはまた別の記事に書こうかと思います。
最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問い合わせにておねがいいたします。
「ε-δ論法について」への1件のフィードバック