量子コンピュータを勝手に解説する記事１

こんにちは、今回は量子コンピュータについて勝手に解説していきます。
本稿はこちらで紹介した書籍を参考にしてます。

私が学生時代のときは実用化には来世紀にはなるだろうと言われていた量子コンピュータですが、近年は21世紀半ばには実用化される勢いとなっており、時代の流れを感じます。

こちらで量子コンピュータについて少し触れましたが、本稿では
・どのような動作原理なのか
・なぜ既存コンピュータよりも高速だと言われているのか
・そもそもどんな社会的インパクトがあるのか
について、もう少しふわっと突っ込んで解説していきます。

1)動作原理

用語の統一のため、現在のノイマン型コンピュータ(パソコンやスーパコンピュータなどといったいわゆるコンピュータ)を古典計算機、量子コンピュータを量子計算機とします。
古典/量子という対は、物理学の慣例に由来します。古典だから古いとかそういうわけではなく、量子論を使わない分野を古典物理学、量子論を使う分野を量子物理学とざっくり分類する慣例です。

1-1) 古典計算機

計算機の演算行為はCPUで行われ、CPUは半導体から構成されています。半導体の中で、
・コンデンサの帯電有無
・ある回路の電流の有無
・磁極の向き
などで、
\[ \{0,1\} \]
を表現します。必ず\(0\) or \(1\)どちらかの値をとり、これはブール代数として理想化されます。ブール代数で定義されている基本演算は、
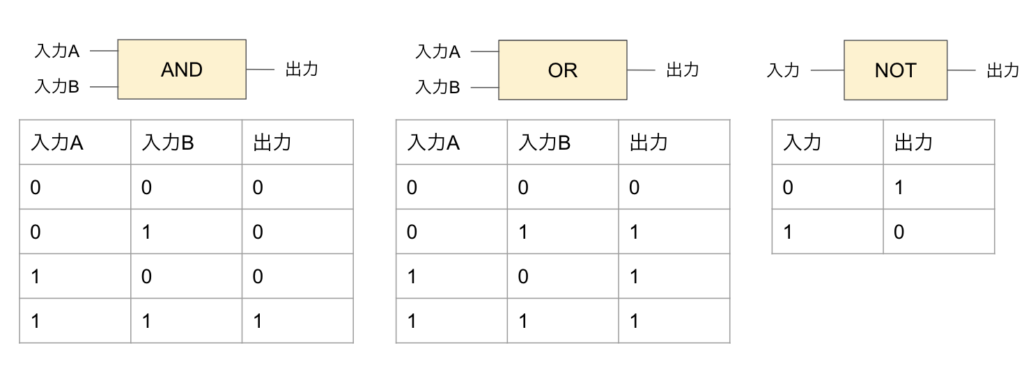
・AND
・OR
・NOT
の３つになり、ブール代数上のいかなる演算も上記の３つの組み合わせで表現できます。つまり３つの演算を使ってビットを操作することで、計算を実施することになります。AND、OR、NOTの演算規則は以下のようなものです。論理ゲートの詳細についてはこちらなども参照ください。

1-2) 量子計算機

古典計算機では\(. \{0,1\} \)のどちらか一方の値をとる前提でした。しかし量子計算機ではこの描像がガラッと変わります。まず古典計算機のビットに相当するところからです。

1-2-1) 量子ビット

物理学では系の状態を記述することから始まります。先の古典計算機のビットであれば、\(0\) or \(1\)が状態を表すことになります。
一方、量子計算機におけるビットのとりうる値は、\(0\) or \(1\)ですが、これは確定した値をとるわけではなく、確率的になります。これは対象のビットを観察してみると、\(0\)の場合もあれば\(1\)の場合もあることを意味しています。
量子計算機でのビットを量子ビット、quantum bit、略してqubitと呼んだりします。

さて、量子ビットについてもう少し踏み込むには量子力学の知識がどうしても必要になります。以下少しまとめておきます。

量子力学ミニマム

1. ケットベクトル
   量子力学では、慣例で状態を表すものを「ケットベクトル」というベクトルで表します。これは
   ・「\(0\)」の状態 \(= |0\rangle\)
   ・「\(1\)」の状態 \(= |1\rangle\)
   となります。\(|0\rangle,|1\rangle\)は線形空間の正規直交基底になります。
   (厳密には線型空間の中でも特別な空間である、「ヒルベルト空間」のベクトルになります。)
   
   
2. ブラベクトルと内積
   ケットベクトルと内積がとれるベクトルをブラベクトルといいます。つまり
   ・\( |0\rangle\)のブラベクトル = \( \langle 0| \)
   ・\( |1\rangle\)のブラベクトル = \( \langle 1| \)
   で表します。
   ※ざっくり言えば、ブラベクトルはケットベクトルの複素転置のイメージで問題ないです。
   
   ブラベクトルとケットベクトルの間に内積を定義でき、\[
   \langle 0|\cdot | 0\rangle = \langle 0 | 0\rangle
   \]などと略記します。
   \(|0\rangle,|1\rangle\)が正規直交基底であることから、\( \langle 0 | 1\rangle = \langle 1 | 0\rangle = 0\)、\( \langle 0 | 0\rangle = \langle 1 | 1\rangle = 1\)になります。
   
   
3. 観測確率
   \( |0\rangle,|1\rangle\)の線形結合もケットベクトルとなります。つまり、\(a,b\)を係数(複素数)として\[
   |\psi\rangle = a|0\rangle + b|1\rangle
   \]もケットベクトルになります。この状態\(\psi\)において、\(0\)を観測する確率は\[
   |\langle 0|\psi\rangle|^2 = \left|\langle 0 |\Big(a|0\rangle + b|1\rangle \Big)\right|^2 = |a|^2
   \]となります。同様にして\(|\langle 1|\psi\rangle|^2 = |b|^2\)となり、また自分自身との内積は\(\langle \psi | \psi \rangle = 1\)であるから、条件として\[
   |a|^2 + |b|^2 = 1
   \]が成り立つことになります。これは\(|0\rangle \)、\( |1\rangle \)を観測する確率の合計が\(1\)であることと一致しています。
   
   
4. 演算子
   状態\( |\psi\rangle\)に対して、何かしら操作するものを作用素、または演算子といいます。
   ※数学寄りの人は作用素、物理/化学寄りの人は演算子と言うことが多いです。
   
   演算子を\(X\)として、これが状態\( |\psi\rangle\)に作用させることを\[
   X|\psi\rangle
   \]と表します。
   またゼロでない係数\(a\in \mathbb{C}\)が存在して\[
   X|\psi\rangle = a|\psi\rangle
   \]となるとき、\(a\)を固有値、そのときの\(|\psi\rangle\)を固有ベクトルと言います。
   量子力学では物理量の観測値は演算子の固有値となります。観測できるには固有値は実数である必要があり、その性質を「自己共役性」といいます。
   
   ※これまた数学寄りの人は自己共役性といい、物理/化学寄りの人は「エルミート性」と言ったりします。関数解析学では自己共役性の方がエルミート性より強い条件ですが、普段の計算ではそこまで気にする必要はないです。自己共役やエルミート等の定義について詳しく知りたい方はこちらも参考にしてください。
   
   状態の観測(いわゆる測定)についても演算子で記述することができます。射影演算子と呼ばれるもので、固有状態\(|a\rangle , a=0,1\)を観測するような演算子は\[
   P=|a\rangle\langle a |
   \]で表すことができます。
   
   
5. 時間発展
   時間発展というのは、時々刻々状態が変わることをいいます。例えば時刻\( t_A\)のケットベクトルを\(|\psi_A\rangle \)とすると、時刻\( t_B (> t_A)\)のケットベクトルを\(|\psi_B\rangle \)は\[
   |\psi_B\rangle = U(t_B,t_A)|\psi_A\rangle
   \]で表されます。\(U(t_B,t_A)\)は
   ・\(|\psi_B\rangle \)と\( |\psi_A\rangle\)のノルムが等しいこと(等長性)
   ・すべての\(|\psi_B\rangle \)は、時間発展前の状態\(|\psi_A\rangle \)をもつ(全射性)
   ことから、ユニタリ演算子となります。
   
   
6. 合成積
   複数のqubitを表すには合成積を表す記号「\( \otimes \)」を使って合成します。2qubitを表すには\[
   |\psi\rangle \otimes |\varphi\rangle\]
   と表現するかたちになります。
   複数のqubitあって、いちいち\( \otimes \)を書くのがめんどくさい場合は\[
   |\psi\rangle |\varphi\rangle ,\ |\psi\varphi\rangle
   \]と略記することも多いです。
   ※「\( \otimes \)」は一般にテンソル積とよばれていますが、ベクトルをいい感じに並べて表記/演算できるようにするにはテンソル積という数学が必要となる、というイメージで問題ないです。
   
   演算子のテンソル積、というのも重要です。例えば\(A\otimes B\)という作用素を\(|\psi\rangle \otimes |\varphi\rangle\)に作用させると、\[
   A\otimes B(|\psi\rangle \otimes |\varphi\rangle)
   = A|\psi\rangle \otimes B|\varphi\rangle
   \]というように、\(|\psi\rangle\)には演算子\(A\)、\(|\varphi\rangle\)には演算子\(B\)を作用させた結果のテンソル積をとることと等しくなります。
   
   

かなり端折ってますが、以上が量子力学の結果をざっとまとめたものです。なんで線型空間やヒルベルト空間といったものを持ち出すのか？、複素数がなぜ出てくるのか？とよく聞かれるのですが、なんでかはぶっちゃけわかりません。無数の実験結果や理論的考察から上記のようにするとうまく説明できるから、というのが解答です。この世界は思ったほど単純にできているわけではないようです。

(もちろん量子力学では数学、特に線形代数や関数解析等を駆使して厳密に定義されています。その際の最低限の要請/公理の部分が直観的でないと言う感じです。)

qbitの担い手となる物理的実体の代表的なものは、光子の偏光状態や電子のスピン等が挙げられます。

長くなってきましたので、本稿はここで切りたいと思います。

最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問合せにてよろしくおねがいいたします。