こんにちは、前回引き続き、量子コンピュータの動作原理から勝手に解説していきます。
今回は量子ゲートからです。
1-2-2) 量子ゲート
古典計算機ではビット操作を AND、OR、NOTという演算で実施してました。量子計算機でもビット操作する演算が存在します。すこし紹介していきます。
基本的な考え方は古典計算機と同じです。入力に対して、何かしらの演算をして、出力するというものです。

具体例をいくつか挙げてみます。
・NOTゲート
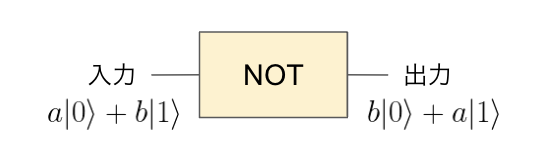
入力のqubitを\( a|0\rangle +b|1\rangle \)とします。NOT演算を施すと\[
b|0\rangle +a|1\rangle
\]のように係数が反転するものになります。
・アダマールゲート
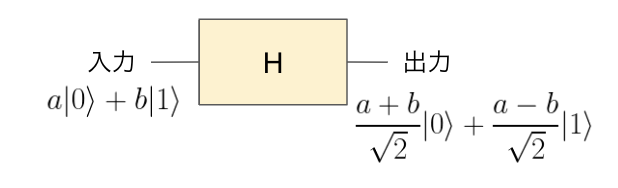
これは量子計算機特有のゲートです。入力のqubitを\( a|0\rangle +b|1\rangle \)にアダマールゲート\(H\)(慣例でアダマールの頭文字をとって\(H\)で表すことが多い)を作用させると、\[
\frac{a+b}{\sqrt{2}}|0\rangle + \frac{a-b}{\sqrt{2}}|1\rangle
\]となるものになります。
1-2-3)量子ゲート(複数qubit)
本稿は複数ビットの場合から解説していきます。
・CNOTゲート(制御NOTゲート)
2qubitを入力とする量子ゲートです。これを\(|\psi\varphi\rangle\)とします。これは制御ビットが\(|\psi\rangle\)で、標的ビットが\(|\varphi\rangle\)となるものです。
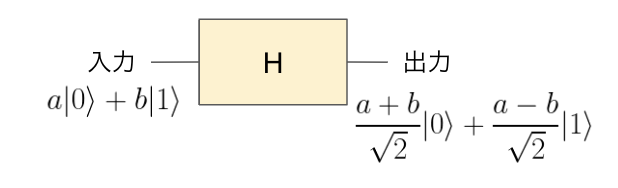
このときの出力\[
|\psi’\rangle|\varphi’ \rangle = \mathrm{CNOT} |\psi\rangle|\varphi\rangle
\]は、制御ビットはとくに変更を受けず、制御ビットが\(|1\rangle\)だった場合だけ、標的ビット\(|\varphi\rangle\)を反転させるもので、\(\mathrm{NOT}\)演算子を\(X\)とすると\[
|\psi’\rangle|\varphi’\rangle = \mathrm{CNOT} |\psi\rangle|\varphi\rangle
=|\psi\rangle X^{\psi}|\varphi\rangle
\]となります。
ここで\(X^{\psi}\)というのは、\(\psi\)のとりうる値は\( \{0,1\}\)なので、
・\(X^0 = I\)で恒等演算子となり、
・\(X^1 = X\)で、NOT演算子になる
と言う感じです。
入力が複数ビットになってくると流石にちょっとわかりづらくなるので、ベクトルを成分表示するようにします。このとき演算子は行列で表現できるので、イメージしやすくなるかと思います。
ケットベクトルを\[
|0\rangle = \binom{1}{0} ,\ |1\rangle = \binom{0}{1}
\]とすると、その任意の線形結合は\[
a|0\rangle + b|1\rangle = \binom{a}{b}
\]と表記できます。ブラベクトルは、ケットベクトルの複素転置でしたから、\[
\langle 0 | = (1,0) , \ \langle 1 | = (0,1)
\]となります。
NOT演算子\(X\)はビットを反転させるもので、\[
X\left( a|0\rangle + b|1\rangle \right) = X\binom{a}{b}
\]が\[
b|0\rangle + a|1\rangle = \binom{b}{a}
\]に等しくなるので、NOT演算子\(X\)は\[
X=\begin{pmatrix}
0 & 1 \\
1 &0
\end{pmatrix}
\]といった行列表記ができます。
2つqubit\(|00\rangle = |0\rangle \otimes |0\rangle\)はテンソル積で定義されており、成分表示すると以下のようになります:\[
|00\rangle = \begin{pmatrix}
1 \\
0 \\
0 \\
0
\end{pmatrix},
|01\rangle = \begin{pmatrix}
0 \\
1 \\
0 \\
0
\end{pmatrix},
|10\rangle = \begin{pmatrix}
0 \\
0 \\
1 \\
0
\end{pmatrix},
|11\rangle = \begin{pmatrix}
0 \\
0 \\
0 \\
1
\end{pmatrix}
\]
ゆえ、任意のベクトルはこれらの線形結合で表すことができるので、\[
a|00\rangle + b|01\rangle + c|10\rangle +d|11\rangle
= \begin{pmatrix}
a \\
b \\
c \\
d
\end{pmatrix}
\]と表記することができます。
さて、CNOT演算子は制御ビットが\(1\)の場合のみ、標的ビットを反転させるものでした。これを行列にすると\[
\mathrm{CNOT} = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
\end{pmatrix}
\]となります。実際、\[
\mathrm{CNOT}|\psi \varphi\rangle = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
\end{pmatrix} \begin{pmatrix}
a \\
b \\
c \\
d
\end{pmatrix} = \begin{pmatrix}
a \\
b \\
d \\
c
\end{pmatrix}
\]となることから、たしかに制御ビットが\(1\)の場合のみ、標的ビットを反転することがわかります。
ちょと長くなりましたが、以上がCNOTゲートになります。
・アダマールゲート&CNOTゲート
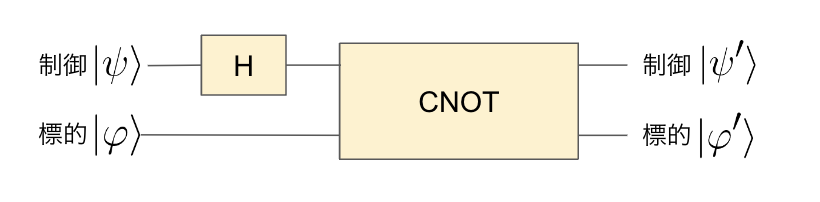
上記のようなゲートを考えます。\(|\psi\rangle = a|0\rangle + b|1\rangle\)、\( |\varphi\rangle = c|0\rangle + d|1\rangle\)とおきます。アダマールゲートを通った後の状態\(H|\psi\rangle \otimes |\varphi\rangle \)は、\[
H|\psi\rangle \otimes |\varphi\rangle =\left( \frac{a+b}{\sqrt{2}}|0\rangle + \frac{a-b}{\sqrt{2}}|1\rangle \right)\otimes (c|0\rangle + d|1\rangle) \\
= \frac{(a+b)c}{\sqrt{2}}|00\rangle + \frac{(a+b)d}{\sqrt{2}}|01\rangle
+ \frac{(a-b)c}{\sqrt{2}}|10\rangle + \frac{(a-b)d}{\sqrt{2}}|11\rangle
\]となります。これにCNOTゲートをかますと\[
\mathrm{CNOT}\left( H|\psi\rangle \otimes |\varphi\rangle \right)
= \frac{(a+b)c}{\sqrt{2}}|00\rangle + \frac{(a+b)d}{\sqrt{2}}|01\rangle
+ \frac{(a-b)d}{\sqrt{2}}|10\rangle + \frac{(a-b)c}{\sqrt{2}}|11\rangle
\]となります。ここで、例えば、初期状態として\( |\psi\rangle = |\varphi\rangle = |0\rangle \)の場合\[
\mathrm{CNOT}\left( H|\psi\rangle \otimes |\varphi\rangle \right)
=\frac{1}{\sqrt{2}}\left( |00\rangle + |11\rangle \right)
\]となります。
ここで、ちょと上記結果をよく見てみると奇妙なことがわかります。もし制御ビットが\( |0\rangle \)だった場合、標的ビットは\( |0\rangle \)となり、制御ビットが\( |1\rangle \)だったら標的ビットは\( |1\rangle \)となります。つまり制御ビットを見た途端に標的ビットの状態がわかることになります。このような非局所な相関性を量子もつれ、エンタングルメントと呼びます。
これは制御ビットと標的ビットがどれだけ離れていても成立します。極論ですが、原理的には宇宙の端から端くらい離れていても成立します。
換言すれば、制御ビットと標的ビットが宇宙の端から端まで離れていても、制御ビットを観測すれば瞬時に標的ビットの状態がわかることになります。
※混同してはいけないのが、情報伝達が瞬時にできるわけではありません。結局制御ビットを観測した人が標的ビットに伝えるためには通常の通信をする必要がありますが、これは光速を超えることはできないためです。
初めて聞くとかなり奇妙に聞こえるかもしれません。実際、アインシュタインと数人の物理学者たちはこれはおかしいと意見していたほどです。(EPRパラドックス)
その後1980年代になり、アスペという物理学者が行った実験により、量子もつれは正しいと結論づけられました。この成果でアスペは2022年にノーベル物理学賞を受賞してます。
量子もつれの性質を積極的に応用した通信方法が量子テレポーテーションになります。
他にも量子ゲートはいろいろありますが、今回は以上です。
最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問合せにてよろしくおねがいいたします。
「量子コンピュータを勝手に解説する記事2」への1件のフィードバック