1回目、2回目に引き続き量子コンピュータの基礎について勝手に解説していきます。
本稿もこちらで紹介した書籍を参考にしてます。
2)古典計算機より量子計算機が速い理由
本稿は量子計算機が古典計算機より早い理由について軽く説明していきます。
最初に結論をいうとビット演算レベルで並列計算ができるためです。これについて以下説明していきます。
ちなみに古典計算機でもマルチスレッドによる並列処理ができますが、CPUのビット演算レベルでは直列です。スレッドAの処理待ち時間をスレッドBの演算時間にあてる感じで、人間からみると並列で処理しているように見えるが、CPUのビット演算レベルでは直列で処理しています。
2-1)並列処理のイメージ
例えば以下のような量子ゲートを考えます.

ここで\( U_f \)は何かしらの演算するゲートで、\[
U_f|x\rangle |y\rangle = |x\rangle |y \oplus f(x)\rangle
\]とします。ここで\( y \oplus f(x) \)は排他的論理和を表します。
初期状態として\( |\psi\rangle = |\varphi\rangle = |0\rangle \)とすると、\[
U_f\Big(H|0\rangle\otimes |0\rangle \Big)
=U_f\Big( \frac{1}{\sqrt{2}}\big( |0\rangle |0\rangle +|1\rangle |0\rangle \big) \Big) \\
= \frac{1}{\sqrt{2}}\Big( |0\rangle |f(0)\rangle + |1\rangle |f(1)\rangle\Big)
\]となります。
この結果をみると、\(U_f\)を一度演算するだけで、1つの状態に\(f(0),f(1)\)両方の値を含むことになります。量子計算機特有の結果になります。
さらに拡張して以下のような量子ゲートを考えます。
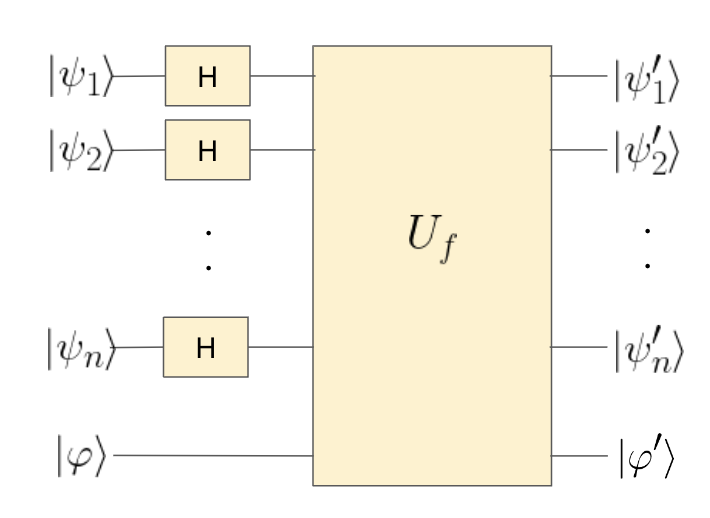
さきほどと同様に、初期状態を\( |\psi_1\rangle = |\psi_2\rangle = \cdots = |\psi_n\rangle =|\varphi\rangle =|0\rangle \)として、計算すると\[
H^n|\psi_1\rangle|\psi_2\rangle\cdots|\psi_n\rangle =H|0\rangle H|0\rangle\cdots H|0\rangle \\ =\frac{|0\rangle + |1\rangle}{\sqrt{2}}\otimes \frac{|0\rangle + |1\rangle}{\sqrt{2}}\otimes \cdots \otimes \frac{|0\rangle + |1\rangle}{\sqrt{2}} \\ = \left(\frac{1}{\sqrt{2}}\right)^n\Big( |00\cdots 0\rangle + |00\cdots 1\rangle + \cdots + |11\cdots 1\rangle\Big)
\]となります。これに\(U_f\)を演算させると、\[
U_F(H^n|\psi_1\rangle|\psi_2\rangle\cdots|\psi_n\rangle\otimes |\varphi\rangle)\\
= U_f\left(\left(\frac{1}{\sqrt{2}}\right)^n \Big( |00\cdots 0\rangle + |00\cdots 1\rangle + \cdots + |11\cdots 1\rangle\Big)|0\rangle \right)\\
= \left(\frac{1}{\sqrt{2}}\right)^n \Big( |00\cdots 0\rangle |f(0)\rangle + |00\cdots 1\rangle |f(1)\rangle + \cdots + |11\cdots 1\rangle |f(2^n-1)\rangle \Big)
\]となります。
今後のため表記の簡略化をします。\(00\cdots 0 = 0\)、\(00\cdots 1 = 1\)、 \(11\cdots 1 =1\cdot 2^{n-1}+ \cdots +1\cdot 2^1 + 1\cdot 2^0=2^n-1\)である(つまり二進法である)ことに注意して、\[
|00\cdots 0\rangle + |00\cdots 1\rangle + \cdots + |11\cdots 1\rangle = \sum_{x=0}^{2^n-1}|x\rangle
\]と表現できます。この表示を使うと上記は\[
U_F(H^n|\psi_1\rangle|\psi_2\rangle\cdots|\psi_n\rangle\otimes |\varphi\rangle)
=\left(\frac{1}{\sqrt{2}}\right)^n \sum_{x=0}^{2^n-1}|x\rangle|f(x)\rangle
\]と簡潔に表現することができます。
さて上記の結果の示唆していることは、\(n\)個の\(f(x)\)の値を\(U_f\)1回の演算で得られ、量子ビットが多いほど指数関数的に\(f(x)\)の値を得られることになります。
もちろんどうやって全ての\(f(x)\)を観測するのか、という問題は残りますが、このようなビット演算レベルで並列計算ができることが、量子計算機が早いと言われる理由の1つになります。
そしてこの並列計算をうまく用いたアルゴリズムもすでに開発されており、
・ドイチュ・ジョザのアルゴリズム
・ショアのアルゴリズム
があります。参考までに以下で紹介します。
2-2)ドイチュ・ジョザのアルゴリズム
ドイチュ・ジョザのアルゴリズムは実用的なアルゴリズムではなく、人工的な問題になります。とはいえ量子計算機が威力を発揮する簡単な例で、教育的なものですので、紹介します。
ある関数\( \ f: \{0,1\}^n \ni x \rightarrow f(x) \in \{0,1\} \)が存在するとします。これが定数関数かバランス関数であるかを瞬殺で判定するアルゴリズムが表題のものとなります。
ここで、\(f\)は\(n\)ビット列\(x\)を入力にして、\(f(x)\)が\( 0\) or \(1\)を出力する関数で、これが定数関数であるとは、任意の入力\(x\)に対して、\(f(x)=0\)もしくは\(f(x)=1\)となるものです。バランス関数であるとは、とりうる\(x\)のうち、ちょうど半分が\(f(x)=0\)となり、\(f(x)=1\)となるものになります。
ということで、現実問題として\(f\)が定数関数かバランス関数かを判定しなきゃいけないケースはほぼないので、あくまで人工的な問題、という感じです。
さて以下のような量子回路を考えます。
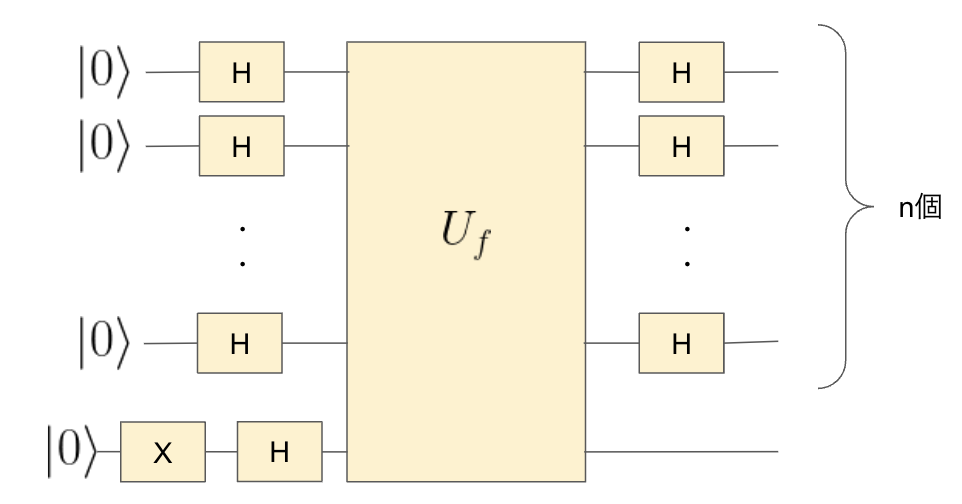
初期状態としては、制御ビット\( \ |0\rangle ^n\)、標的ビット\( \ |0\rangle\)との合成\(\ |0\rangle ^n |0\rangle\)となります。標的ビットにNOT演算子を作用させると\( |0\rangle ^n |1\rangle \)となります。これにアダマール演算子を作用させると\[
H^{n+1}|0\rangle ^n |1\rangle
=\left(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\right)^n\left(\frac{|0\rangle – |1\rangle}{\sqrt{2}}\right)
=\left(\frac{1}{\sqrt{2}} \right)^{n} \sum_{x=0}^{2^n-1}|x\rangle\left(\frac{|0\rangle – |1\rangle}{\sqrt{2}}\right) \\
= \left(\frac{1}{\sqrt{2}} \right)^{n+1}\sum_{x=0}^{2^n-1}\Big(|x\rangle|0\rangle – |x\rangle|1\rangle\Big)
\]となります。これに\(U_f\)を作用させると、\[
U_f\Big(H^{n+1}|0\rangle ^n |1\rangle \Big)
= \left(\frac{1}{\sqrt{2}} \right)^{n+1}\sum_{x=0}^{2^n-1}\left(|x\rangle|0\oplus f(x)\rangle – |x\rangle|1\oplus f(x)\rangle\right) \\
= \left(\frac{1}{\sqrt{2}} \right)^{n+1}\sum_{x=0}^{2^n-1}(-1)^{f(x)}|x\rangle\Big(|0\rangle – |1\rangle\Big)
\]となります。
さらに再度制御ビットにアダマール演算子を作用させるのですが、これはやや技巧的になります。最終的な結果を書くと\[
\left(\frac{1}{\sqrt{2}}\right)^{2n+1}\sum_{x,y=0}^{2^n-1}(-1)^{f(x)}(-1)^{\langle x,y\rangle}|y\rangle
\]となります。ここで、\[ \langle x,y\rangle = \sum_{i=1}^{n}x_iy_i \mod 2\]であり、2で割った余りです。
この状態の\(|0\rangle^n\)の振幅を求めると\[
\left|\left(\frac{1}{\sqrt{2}}\right)^{2n}\sum_{x=0}^{2^n-1}(-1)^{f(x)} \right|^2
\]となりますが、\(f\)が定数関数であれば、上記は1、\(f\)がバランス関数であれば、0になります。したがって\(U_f\)の演算1回で、定数関数かバランス関数かを判定することができる、と言う感じになります。
長くなってきたので今回はこれで終わります。
ショアのアルゴリズムは別途紹介したいと思います。
最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問合せにてよろしくおねがいいたします。