量子コンピュータを勝手に解説する記事 トポロジカル量子計算について

本日はトポロジカル量子コンピュータについて勝手に概説していきます。

本稿はややマニアックですが、トポロジカル量子計算について、ふんわり解説していきたいと思います。今回はこちらを参考にしてます。
(トポロジカル量子計算は現状日本語の書籍がないので、どなたか日本語で解説した書籍を書いてほしい。。。)

トポロジカル量子計算はその名の通り、トポロジーすなわち位相幾何学的性質を用いた量子計算になります。

従来の量子ゲートは、スピンや光子などを用いて量子ビットを作成しますが、量子ビットは外部ノイズに非常に敏感で壊れやすく、エラー補正が課題となっています。

トポロジカル量子計算はエニオンと呼ばれる粒子を量子ビットの構成要素にすることで、仕組み的に外部ノイズに強い量子計算を行なえると期待されています。

トポロジカル量子コンピュータに注力しているのがMicroSoftであり、Station Qという研究機関を立ち上げてトポロジカル量子計算の実現に力を注いでいる状況です。2018年にエニオンの候補となるマヨラナ準粒子がトポロジカル超伝導体の表面に存在するという内容の論文が出て、トポロジカル量子コンピュータの実現に一歩近づいたと思いきや、論文のデータに人為的な操作があったとして2021年に撤回されてしまっています。

トポロジカル量子計算はハードウェアレベルで耐障害性を具備しているので、一発逆転できる量子計算の方式かと勝手に思っているので、引き続き頑張ってほしいものです。

1)エニオン(Anyon)について

エニオンおよびその交換操作を厳密に記述するには、位相的場の理論(Topological Quantum Filed Theory, TQFT)とよばれる場の量子論の知識が必要となり、私ごときでは太刀打ちできる代物でもないので、以下の記述はあくまで概説になります。

まず3次元系における２粒子系の波動関数\( \psi (\mathbf{r}_1,\mathbf{r}_2) \)を考えます。

このとき２粒子系の位置を入れ替える演算子を\(R\)を定義します。\( \psi (\mathbf{r}_1,\mathbf{r}_2) \)に２回\(R\)を作用させると元に戻るはずなので、

\[
R^2\psi (\mathbf{r}_1,\mathbf{r}_2) =\psi (\mathbf{r}_1,\mathbf{r}_2)
\]

となります。これから演算子\(R\)は

\[
R^2 = 1 \\
\Leftrightarrow R=\pm 1
\]

となります。\(R=+1\)がボソンに相当し、\(R=-1\)がフェルミオンに相当します。

あっさりしてますが、以上が３次元での粒子の交換です。３次元はあまり交換する経路など考える必要はなかったのですが、２次元系の場合はそう簡単ではありません。以下少し詳しくみていきます。

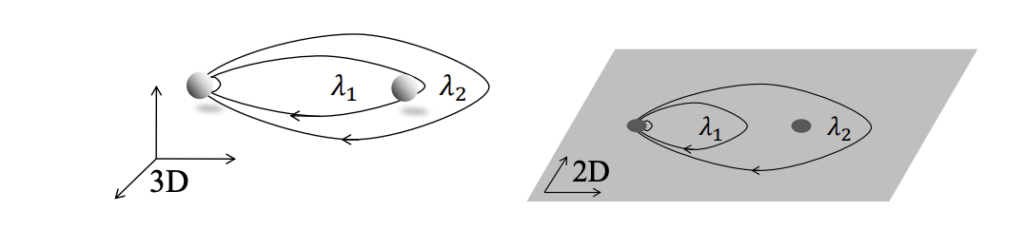
※図はこちらのP4から拝借。

上の図の\(\lambda_1\)は経路の中に別粒子を含まない経路で、\(\lambda_2 \)は経路の中に別粒子を含む経路です。３次元の場合、\(\lambda_2 \)は\(\lambda_1 \)に連続的に縮小させることができ、さらに一点にまで縮小させることができます。(これを位相幾何学では可縮であると言ったりします。)\(\lambda_2 \)を\(\lambda_1 \)に連続的に変化する際、粒子にぶつかりそうになったら、粒子のほんの少し上ないし下を通るようにすればよいからです。

一方２次元では\(\lambda_2 \)は\(\lambda_1 \)へ連続的に縮小させることができません。３次元の場合とは異なり、ちょい上 or ちょい下を通るようにすることができないためです。

こうした理由から３次元では当然成立した条件\(R^2=1\)は、２次元では成立しなくなります。このとき交換演算子\(R\)は

\[
R = \left\{\begin{matrix} e^{i\theta} \\ U \end{matrix}\right.
\]

というふうにかけます。ここで\(U\)はユニタリ作用素をあらわします。\(R=\exp(i\theta)\)の場合「Abelian Anyon」(可換エニオン)といい、\(R=U\)の場合を「non-Abelian Anyon」(非可換エニオン)といいます。

これらのエニオンは基底状態と励起状態の間にエネルギーギャップが存在するため安定的に存在します。

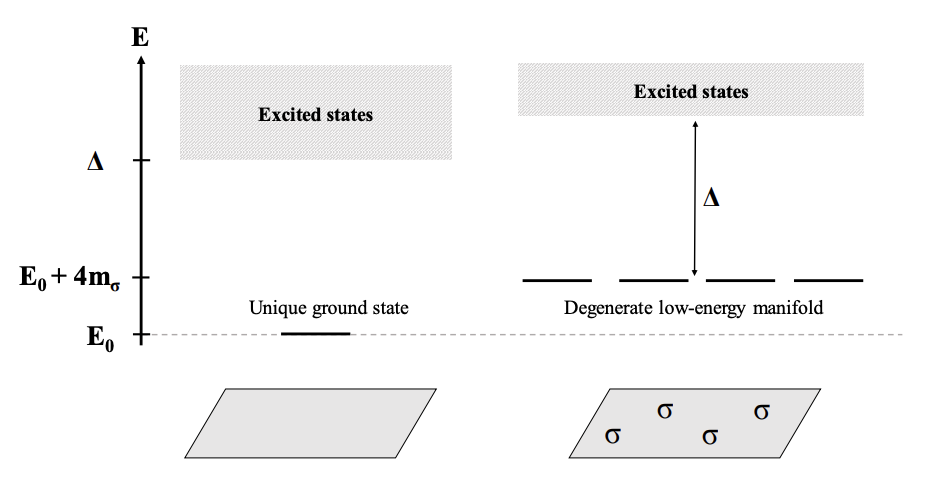
※こちらのP.10より拝借

左のエネルギー準位が可換エニオンの図式であり、右側が非可換エニオンの図式です。

可換/非可換どちらのエニオンに対してもエネルギーギャップが存在することで、外部の擾乱によって、励起されにくい構造となっているのが特徴です。
また可換エニオンの基底状態は縮退していませんが、非可換エニオンの方は一般にエニオンが複数あると縮退した基底状態をとります。

エネルギーギャップ\(\Delta\)を越えないように(物理的には断熱的に変化させるといいます)、エニオンを交換することができます。非可換エニオンの交換の仕方は、数学的には組紐群をなすことが知られており、これを量子計算に応用したのがトポロジカル量子計算になります。

非可換エニオン系の時間発展について少し言及しておきます。\(N\)個の非可換エニオン系において、\(D\)重に縮退した状態を

\[
| \Psi_n(z_1,z_2,..,z_N) \rangle ,\ \ n=1,2,…,D
\]

とおくと、この系のエニオンをいくつか交換したあとの状態は

\[
\sum_{m=1}^D \Gamma_{nm}(\lambda) | \Psi_n(z_1,z_2,..,z_N) \rangle
\]

と表されます。ここで、\(\Gamma\)は非可換エニオンのベリー位相とよばれる量で、

\[
\Gamma(\lambda) = \mathbf{P} \exp\oint \mathbf{A}\cdot d\mathbf{z}
\]

となります。\(\mathbf{P}\)はパスオーダー(すみません、いい感じの訳が出てこない。。)で、\(A,B,C,D\)を演算子、\(x_1\leq x_2\leq x_3 \leq x_4\)とすれば、

\[
\mathbf{P}\left( A(x_3)B(x_1)C(x_4)D(x_2) \right)=B(x_1)D(x_2)A(x_3)C(x_4)
\]

となります。\(\mathbf{A}\)がベリー接続と呼ばれる量で、その成分は

\[
A^j_{k\ell} = \langle \Psi_k(z_1,..,z_N) | \frac{\partial }{\partial z_j} | \Psi_{\ell}(z_1,..,z_N)\rangle
\]

で与えられます。

エニオンの交換が断熱過程である場合、このベリー位相が\(\Gamma(\lambda) \approx F^{-1}R^2F\)というような、組紐群の形に近似できることになります。(このあたりの詳細は別途解説します。)組紐群を量子計算に応用したのがトポロジカル量子計算になります。

※ベリー位相の全体的な説明はこちらが詳しいので、参照してみてください。

エニオンしか辿り着いてないですが、、本日はこれくらいにしておきます。

最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問合せにてよろしくおねがいいたします。