サラリーマンが測度論を勝手に解説する無謀な記事４

本日は前回から引き続きルベーグ積分と測度について解説していきます。

前回ルベーグ積分は、\((X,\mathcal{F},\mu)\)を測度空間として、
\[
\int f(x)\mu(dx) = \sum_{i=1}^{\infty} a_i \mu(A_i), \ \{A_i\}_{i\in\mathbb{N}}\in \mathcal{F}
\]
となるのでした。そしてこれは縦が\(a_i\)、横が\(\mu(A_i)\)の長方形を足し合わせたものでした。\(a_i\)は\(f\)の値ででしたので、そのまま積分の式を解釈すると\(f\)と\(\mu(dx)\)の長方形を足し合わせるとも捉えられます。

ではリーマン積分と何が違うのでしょうか。これについて述べたいと思います。

例として以下の図のような関数\(g(x)\)を見てみます。基本的に前回までの\(f(x)\)と同じ関数ですが、\(x=1/3\)だけ外れ値をもつような関数です。

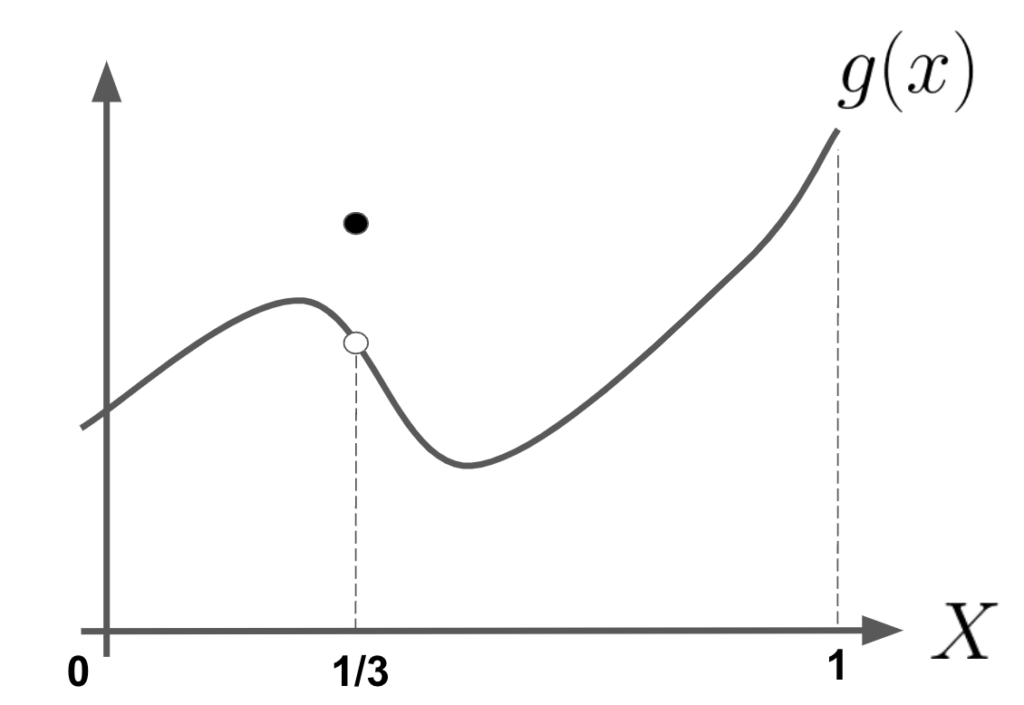
この積分をまずリーマン積分で考えます。\(x=1/3\)で不連続なので、リーマン積分で扱えないのですが、無理やり求めるとすれば
\[
\int_0^{1/3-\varepsilon}g(x)dx + \int_{1/3+\varepsilon}^1 g(x)dx
\]
として、\(\varepsilon\rightarrow 0\)の極限をとる形になります。その結果、\(\int f(x)dx\)と等しくなります。

一方ルベーグ積分は、というと定義から瞬殺で
\[
\int g(x) \mu(dx) = \int f(x)\mu(dx)
\]
が言えます。なぜなら\(x=1/3\)は可算集合のため厳密に\(\mu(x=1/3) = 0\)となり、積分に一切寄与しないからです。

さて次に以下のような関数を考えてみます。

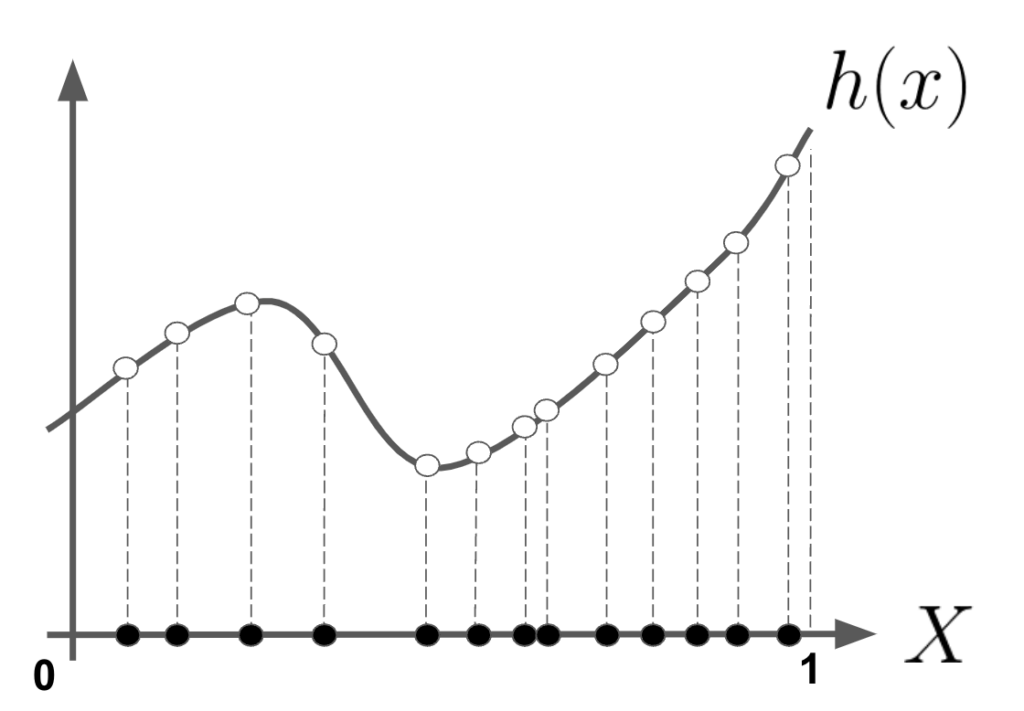
式で書くと
\[h(x) = \left\{\begin{matrix} f(x), \ x \in \{[0,1]内の無理数\}\\
0,\ x\in \{[0,1]内の有理数\} \
\end{matrix}\right.\]
となります。
この関数のリーマン積分ですが、区間\([0,1]\)に有理数は稠密に存在するので、いたるところ不連続になってしまいます。そのため積分が定義できないのです。
※\(A\subset X\)が\(X\)において稠密であるとは、\(x\in X\)をとると\(x\)は\(A\)の元そのものか、もしくは\(x\)のいくらでも近くに\(A\)の元が存在する、という意味です。
上の例でいえば、ある\(x\in [0,1]\)をとると、\(x\)のいくらでも近くに有理数が存在するというものです。

ルベーグ積分を用いると上記\(h(x)\)も積分可能となります。有理数全体の集合は可算集合でしたから、測度\(\mu(x|xは有理数)=0\)となるので、
\[
\int h(x) \mu(dx) = \int f(x)\mu(dx)
\]
が成立します。

以上の概念を定義にしてまとめます。

DEF.7 零集合
\((X,\mathcal{F},\mu)\)を測度空間とする。\(\mu(A)=0\)となる可測集合\(A\in\mathcal{F}\)を零集合という。
ある性質\(P\)が零集合以外で成り立つ場合、ほとんどいたるところで\(P\)が成立する、といい、\(P \ a.e.\)と書く。a.e. はalmost everywhereの略。

\((X,\mathcal{F},\mu)\)を測度空間とし、\(f:X\rightarrow Y\),\(g:X\rightarrow Y\)を可測関数とする。零集合を除いて、
\[
\int f(x)\mu(dx) = \int g(x) \mu(dx)
\]
が成り立つとき、\(f(x) = g(x) \ a. e.\)と表す。
これは同値関係\(\sim \)と捉えることができ、その同値類の代表元を\([f]\)と表す。

上記の同値関係は可測関数全体の集合の考え方につながり、\(L^p\)空間と呼ばれる関数空間につながっていきます。

本日はここまでにします。

最後まで読んでくださりありがとうございます。
質問等はコメント欄かお問い合わせにてよろしくおねがいいたします。