ε-δ論法について　その２

こんにちは、本日は$\varepsilon$-$\delta$論法の続きを勝手に解説していきます。

まず関数の連続について見ていきます。

関数$f(x)$が$x=a$で連続であることの初等的な定義は以下になります。
「$x$が$x\neq a$を満たしながら$a$に限りなく近づいていくとき、$f(x)$も限りなく$f(a)$に近づくときをいい、$\lim_{x\rightarrow a}f(x) = f(a)$と記載する。」

雰囲気的にはこれでなんとく理解できますが、数学的には「限りなく近く」という文言が曖昧です。そこでこちらで数列の収束の定義で用いた、$\varepsilon-\delta$論法を使って、厳密に書き換えます。
結果からいうと

$\forall\varepsilon >0$に対して$\exists \delta>0$が存在して、$|x-a|< \delta$となる$\forall x$に対して、$|f(x)-f(a)|<\varepsilon$が成り立つとき、$f(x)$は$a$で連続であるという。

となります。もっと簡略化すると

$$\forall \varepsilon>0,\exists \delta >0\ s.t. \forall x ,|x-a|<\delta \Rightarrow |f(x) -f(a)|<\varepsilon$$

となります。$s.t$は「such that ~」の略で、「~のような」の意味合いです。

さてこの意味を紐解いていきます。まずはこれを図にすると以下のイメージになります。

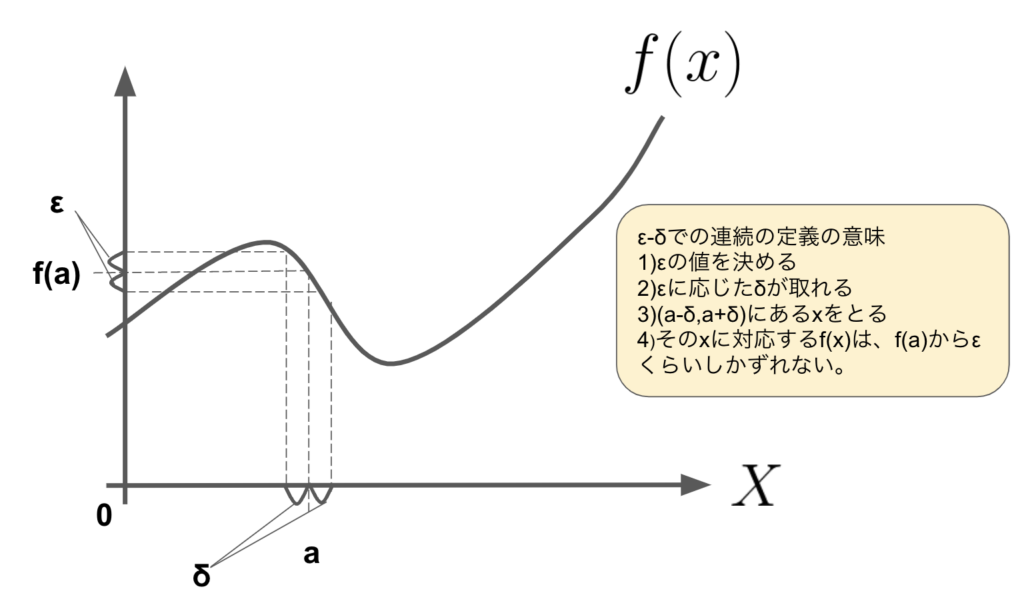
$\varepsilon$の値を決めます。すると$\varepsilon$に応じた$\delta$を決めることができ、$(a-\delta,a+\delta)$の範囲の任意の$x$に対して、$f(x)$は$(f(a)-\varepsilon,f(a)+\varepsilon)$の範囲のどこかに存在するよ、という意味あいです。$a-\delta<x<a+\delta$、$f(a)-\varepsilon<f(x)<f(a)+\varepsilon$を整理すると,$|x-a|<\delta$、$|f(x)-f(a)|<\varepsilon$になります。

連続の定義の意味合いについて、なんとなくイメージはできたでしょうか？

以下、話を具体的にするため、$f(x) = x^2$において$x=a$で連続かどうかを$\varepsilon$-$\delta$で考えてみます。
※もちろん初等的な定義から$\lim_{x\rightarrow a}f(x) = f(a)$となることがわかるので、連続になります。

数列の極限の場合と同じように、まず$\varepsilon >0$を決めます。これはこの程度だったら誤差とみなせるような値で、状況に応じて決めますが、数列の収束の場合と同様、$10^{-4}$や$10^{-6}$というような小さい数になります。

すると$\varepsilon$に応じた、s.t.以下の条件を満たす$\delta$が常に存在すると言ってるのが上の定義です。存在することの証明の１つの方法は、直接具体的にその値を求めればよいので、その値を求めてみます。
※存在の証明で、具体的な値は謎だが、存在を証明できることがしばしばあります。応用上、存在することがわかっても具体的な値がわからないと困ることがよくあるので悩ましいところです。。

さて、
$$|f(x)-f(a)|=|x^2-a^2|=|(x+a)(x-a)|<|x+a|\delta$$
となりますが、$|x+a|$をうまく不等式を用いて、$\delta$と$a$だけで上から挟めないかを考えます。すると
$$|x+a|=|x-a+2a| \leq |x-a|+2|a|<\delta +2|a|$$
とできるので、
$$|f(x)-f(a)|<|x+a|\delta <( \delta + 2|a|)\delta$$ 。
これが、$\varepsilon$より小さいので、$( \delta + 2|a|)\delta<\varepsilon$で$\delta$を$\varepsilon,a$で表せば、、、といきたくなるのですが、$\delta$の二次不等式となり煩雑となるので、もう一工夫加えます。

ゴールは$\varepsilon$に対して、$\delta >0$の存在を言えればよいのでした。ゆえ、$\delta < 1$と条件を絞っても、その範囲で存在しさえすればよいことになります。$\delta < 1$とおくと$|f(x)-f(a)|<(1+2|a|)\delta<\varepsilon$とでき、$\delta<\varepsilon/(1+2|a|)$となるので、だいぶスッキリします。したがって、$\varepsilon$を与えられたとき、

$$\delta = \min\left\{ 1,\frac{\varepsilon}{1+2|a|} \right\}$$

と$\delta$を取ればよいことになります。したがって、まとめると

$\varepsilon$に対して、$\delta = \min \{ 1, \varepsilon/(1+2|a|)\}$ととれば、$|x-a|<\delta$なる$x$に対して、
$$|f(x)-f(a)| =|(x-a)(x+a)| < \delta(\delta + 2|a|)\leq \delta(1+ 2|a|) \leq \frac{\varepsilon}{1+2|a|}(1+2|a|) =\varepsilon$$

となるから、$f(x)=x^2$は$x=a$で連続であることが言えました。

以上関数の連続の定義を説明してみました。

極限をとるような操作は厳密には全て$\varepsilon$-$\delta$論法で定義されます。
(というか現代の解析学では、極限は$\varepsilon$-$\delta$論法で定義するものなので、「$\varepsilon$-$\delta$論法で」という枕詞すらつけないです。ただし、根底には$\varepsilon$-$\delta$があるが、簡略化のために$\lim$を用いた定義にすることはあります。 )
例えば微分係数$f'(a)$の$\varepsilon$-$\delta$論法での定義は、

$$\forall \varepsilon >0,\exists \delta>0 \ s.t. \forall x,|x-a|<\delta \Rightarrow \left| \frac{f(x)-f(a)}{x-a} – b\right| < \varepsilon$$

をみたすとき、$f(x)$は$x=a$で微分可能であるといい、$b= f'(a)$と書いて、これを微分係数という。

本日はここまでにします。

最後まで読んでいただきありがとうございます。
質問等はコメント欄か問い合わせにてよろしくおねがいいたします。